Cinquantenaire de l'Institut des hautes études scientifiques

J'ai eu la chance de participer au cinquantenaire de l'Institut des Hautes études scientifiques (Bures s/Yvette) ; sans doute un des plus importants centres au monde en mathématiques et en physique mathématique, animé par Jean-Pierre Bourguignon. Toutes les conférences étaient intéressantes, j'en mentionnerais deux.

J'avais déjà évoqué dans ce blog  Marc Chemillier et les "ethnomathématiques" ; il nous parlé du Vanuatu (ex- Nouvelles Hébrides), et des artistes qui y dessinent des tortues sur le sable, voir la vidéo :

Un cycle d'Euler autrement plus compliqué que celui de l'enveloppe ! Mais il respecte lui aussi la règle - un graphe peut être dessiné sans lever la main si et seulement s'il possède zéro ou deux sommets d'ordre impair (celui duquel on part et celui auquel on arrive; si c'est le même point de départ et d'arrivée il y a 0 sommet d'ordre impair ; pour les sommets qui ne sont ni point de départ ni point d'arrivée, on y arrive et on en repart à chaque fois, donc ils sont forcément d'ordre pair).

---

La conférence d'Etienne Ghys était totalement nouvelle pour moi - le titre en était alléchant « 3264 » (lire  cette conférence sur la page d'E.Ghys). Il s'agissait principalement de coniques (la conique correspond à la coupe d'un sablier par un plan : ce peut être une ellipse, une parabole ou une hyperbole). Il nous a rappelé un résultat de Chasles (1793-1880) : il existe 3264 coniques tangentes à cinq coniques données dans un plan ! Ces coniques peuvent être réelles ou complexes ;  les mathématiciens ont cherché à savoir lesquelles pouvaient être réelles.
En 1997, Les mathématiciens Ronga, Tognoli et Vust ont exhibé un cas où ces 3264 coniques sont réelles (chacune des arêtes d'un pentagone supporte une hyperbole, cf. figure). En 2005, un jeune mathématicien français, Jean-Yves Welschinger, a démontré, pour les tangentes à cinq ellipses non sécantes dans un plan, qu'il existait au moins 32 coniques réelles tangentes (qu'on peut effectivement dessiner), et a démontré l'optimalité de son théorème : il en existe au moins 32 pour toute configuration des ellipses, mais il y a des configurations où il n'y en a qu'effectivement 32...

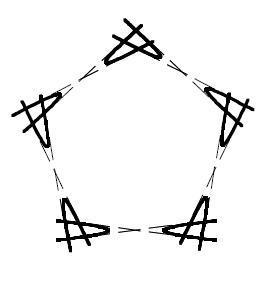
Ghys a qualifié ce résultat de « beau théorème » au sens que lui donnait Hilbert : 1) simple à énoncer ; 2) faisant suite à une longue histoire (c'est la cas après les coniques de Gauss et de Chasles) ; 3) faisant appel à des méthodes nouvelles (Welschinger utilise la méthode des jauges, inspirée de la physique théorique récente ; nul doute que Chasles ignorait cette méthode, idem. Fermat & Wiles) ; 4) engendrant de nouveaux développements possibles (c'est le début d'une « géométrie énumérative réelle »).

Une belle après-midi, avec de nombreux collégiens et lycéens, montrant des mathématiques vivantes et animées.