Le problème du bourdon revisité

Le "problème du bourdon" vous connaissez ? C'est un grand classique des problèmes de mathématiques accessible dès le collège.

Voici l'énoncé :

Deux trains roulent l'un vers l'autre sur deux rails parallèles, à la même vitesse. Un bourdon (ou une mouche, ou toute bestiole volante capable de rouler plus vite que des trains...) s'amuse à faire l'aller-retour entre les deux trains. Au début de l'expérience, les trains sont séparés d'une distance donnée. Le but est de calculer la distance parcourue par le bourdon jusqu'à ce les trains se croisent.

Ce qui est étonnant avec ce problème c'est que :
1. un non mathématicien va trouver un raisonnement très simple pour résoudre le problème en trois lignes ;
2. un mathématicien pense tout de suite à un sombre calcul de limite de série...

Et comme, je suis un peu mathématicien sur les bords, je vous propose la résolution compliquée avec une dose de bonne humeur et adaptée avec l'actualité du moment.

Sommaire

Définition du problème

Le problème du bourdon revisité L'un des trains sera remplacé par le super-héro "Kid Flash" qui a la formidable aptitude de se déplacer à des vitesses proches de la célérité de la lumière. On supposera donc que Kid Flash se déplace à la vitesse constante, sur une trajectoire rectiligne, d'un point O vers un point A situé à une distance 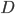, à l'autre bout de l'Univers (cf schéma ci-après).

Le problème du bourdon revisité Le bourdon sera substitué par un autre super-héro "Jimmy Neutron" à qui je prêterai, à titre exceptionnel dans le contexte de cet article, puisse-t-il me pardonner, la capacité de se déplacer à la vitesse d'un neutrino, supérieure à celle de la lumière si l'on en croit les actualités récentes du CERN. On supposera que Jimmy se déplace à la vitesse 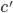sur la même ligne reliant le point O au point A.

Kid Flash et Jimmy Neutron partent ensemble du point O.

Ainsi, pendant que le valeureux Kid Flash fait sa promenade à travers l'Univers, l'impétueux Jimmy Neutron effectue des aller-retours entre son collègue et le point A.

L'objectif est de calculer la distance totale parcourue par Jimmy Neutron jusqu'à ce que Kid Flash atteigne son point d'arrivée.

Le problème obtenu est équivalent au problème original avec deux trains et un bourdon, mais les calculs sont plus simples.

Remarque : je sens venir les physiciens relativistes. OUI, je suppose que la mécanique Newtonienne reste valable pour des valeurs de et 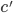proches de la célérité de la lumière, et OUI, c'est de la science-fiction.

Passons maintenant aux choses sérieuses...

Notations

La droite (OA) est orientée positivement du point O vers le point A.
Soient ensuite,

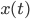: la position de Kid Flash à un instant t. Kiddy se déplaçant à la vitesse de O vers A, on a immédiatement $x(t)=c\times t$ .
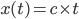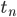: le temps correspondant à la 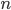-ième rencontre des deux super-héros, et on pose 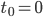et .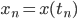
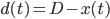, la distance restant à parcourir par Kid Flash à un instant 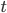pour atteindre A. On pose 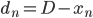, la distance séparant les deux protagonistes de A au 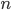-ième point de rencontre. On a donc 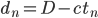(1).
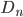: la distance totale parcourue par Jimmy au 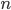-ième point de rencontre.
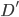: la distance parcourue par Jimmy Neutron quand Kid Flash atteint son point d'arrivée.

Analyse du problème

Le problème du bourdon revisité
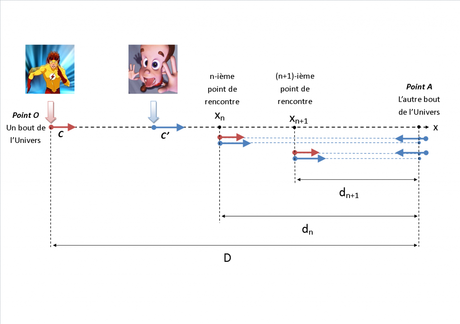
Pendant que Jimmy va de O vers A puis revient chatouiller les narines de Kid Flash, ce dernier avance et continue son chemin. A chaque rencontre, Kid Flash se rapproche de son point d'arrivée alors que Jimmy effectue des allers-retours de plus en plus court. La distance parcourue par Jimmy Neutron à la 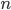-ième rencontre est donc la somme des longueurs des allers-retours qu'il a effectué.

Détaillons un peu. Au premier point de rencontre, Mr Neutron a parcouru la distance 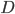pour aller en A, puis il revient vers Kid Flash et l'atteint après avoir parcouru la distance 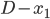D-x_1 , donc la distance totale parcourue par Jimmy au moment du premier point de recontre est :

D_1=D+(D-x_1)=D+d_1.

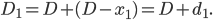
Au second point de rencontre, Jimmy parcourt la distance 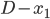D-x_1 pour aller en A, puis il revient vers Kid Flash et l'atteint après avoir parcouru la distance 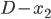D-x_2 , donc

D_2=D_1+(D-x_1)+(D-x_2)=D+2d_1+d_2.

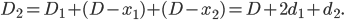
En généralisant au rang 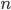¹, on obtient :

$D_n=D+2\displaystyle\sum \limits_{k=1}^{n-1} d_k+d_n,$

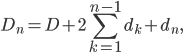
ce qu'on réécrit pour simplifier sous la forme

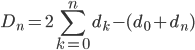$D_n=2\displaystyle\sum \limits_{k=0}^{n} d_k-(d_0+d_n)$ (2).

La distance 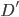à calculer est donc la limite quand 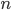tend vers l'infini de la somme des distances parcourue par Jimmy Neutron :

$D'=\displaystyle\lim\limits_{n \to +\infty}D_n.$

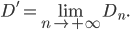
Or, 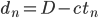d_n=D-ct_n . Il ne nous reste plus qu'à calculer les expressions des instants de rencontres 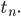t_n. C'est là que ça se corse un poil.

Calcul des instants de rencontres

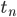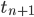Entre deux rencontres consécutives, c'est à dire entre les instants t_n et $t_{n+1}$ , Kid Flash parcourt la distance 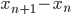$x_{n+1}-x_n$ , et Jimmy Neutron parcourt la distance 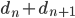$d_n+d_{n+1}$ . Le temps s'écoulant à la même vitesse pour tout le monde², on a donc :

$\displaystyle\frac{x_{n+1}-x_n}{c}=\frac{d_n+d_{n+1}}{c'}.$

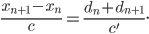
Grâce à la relation (1) (cf section notations), on obtient après quelques lignes de calcul³ :

$t_{n+1}=\displaystyle\frac{c'-c}{c'+c}t_n+\frac{2D}{c'+c}.$

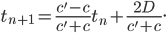
Posons nous un moment sur cette relation. C'est une relation de récurrence affine, ni géométrique, ni arithmétique. C'est en fait une relation de récurrence arithmético-géométrique du type

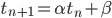$t_{n+1}=\alpha t_n+\beta$ , avec 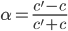$\alpha=\displaystyle\frac{c'-c}{c'+c}$ et $\beta=\displaystyle\frac{2D}{c'+c}.$

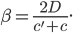
Ce type de relation se rencontre fréquemment dans la modélisation des flux (d'argent ou de population)⁴.

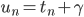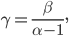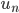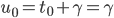Pour obtenir le terme général d'une suite de ce type, on pose $u_n=t_n+\gamma$ avec $\gamma=\displaystyle\frac{\beta}{\alpha-1},$ et on démontre⁵ que u_n est une suite géométrique de raison $\alpha$ et de premier terme $u_0=t_0+\gamma=\gamma$ . On obtient donc le terme général 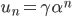$u_n=\gamma\alpha^n$ , et en inversant la relation on trouve :

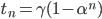$t_n=\gamma(1-\alpha^n)$ (3)

avec, dans notre cas, 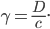$\gamma=\displaystyle\frac{D}{c}.$

Maintenant qu'on a trouvé l'expression de nos temps de rencontres, il ne nous reste plus qu'à injecter tout ça dans la relation (2) pour conclure.

Calcul de la distance parcourue

Revenons un peu en arrière.

On a 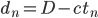d_n=D-ct_n , d'où, en injectant l'expression obtenue précédemment pour t_n ,

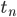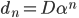$d_n=D\alpha^n \quad$ (4).

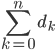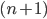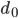Dans la relation (2), on a le terme $\displaystyle\sum \limits_{k=0}^{n} d_k$ . C'est la somme des (n+1) premiers termes d'une suite géométrique de raison $\alpha$ et de premier terme d_0 . Elle vaut donc

$\displaystyle\sum \limits_{k=0}^{n} d_k=d_0\displaystyle\frac{1-\alpha^{n+1}}{1-\alpha} \quad (5).$

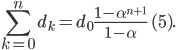
En injectant les relations (4) et (5) dans (2), on obtient, après quelques lignes de calcul⁶ :

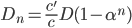$D_n=\displaystyle\frac{c'}{c}D(1-\alpha^n)$ (6).

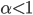Comme $\alpha<1$ <1 " title="Le problème du bourdon revisité" /><1 " /><1 " title="Le problème du bourdon revisité" /><1 " style="vertical-align: middle; border: none; " class="tex" /><1 " />, 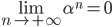$\displaystyle\lim\limits_{n \to +\infty}\alpha^n=0$ , et par conséquent :

$D'=\displaystyle\frac{c'}{c}D.$

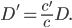
Retour au problème initial

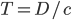Afin de valider les résultats obtenus, je vous propose la solution simple. Le processus prend fin lorsque Kid Flash atteint le point A. Comme il voyage à la vitesse , il met le temps T=D/c , pour parcourir cette distance.

Première remarque : on retrouve bien que 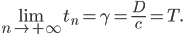$\displaystyle\lim\limits_{n \to +\infty}t_n=\gamma=\frac{D}{c}=T.$

Pendant ce temps 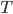, Jimmy Neutron aura donc parcouru à la vitesse 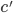, la distance 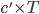$c'\times T$ , ce qui donne bien le résultat annoncé :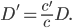 $D'=\displaystyle\frac{c'}{c}D.$

Application numérique

Avec

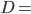1 année lumière soit environ 9500 milliard de km ;
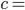célérité de la lumière, soit environ 300 000 km/s ;
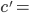300.006 km/s.

On obtient :

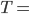31666666,6667 s = environ une année (normal...)
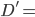9500,19 milliard de km.
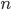
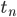(en secondes) 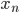(en km) 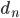(en km) 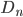(en km)

1 3,166 635 000 320 . 10⁷ 9 499 905 000 950 0,94 9 500 094 999 050

2 3,166 666 663 500 . 10⁷ 9 499 999 999 050 9 500 . 10^-9 9 500 189 999 050

3 3,166 666 666 667 . 10⁷ ~ 9 500 000 000 000 ~ 0 ~ 9 500 190 000 000

Conclusion

L'écart relatif de vitesse entre Kid Flash et Jimmy Neutron est tellement faible (0,02 %) qu'il suffit de trois rencontres très rapprochées du point A pour que le processus touche à sa fin (en arrondissant).

Jimmy Neutron aura uniquement parcouru quelques 190 millions de km en plus que Kid Flash.

Pour conclure, ce frimeur de Jimmy Neutron a beau aller plus vite que Kid Flash, il y a encore de la marge avant qu'il lui foute une raclée au 100 mètres haies.

Pour aller plus loin...

En vérité, Jimmy Neutron ne peut pas du tout se déplacer à la vitesse d'un neutrino ou d'un photon. Tout au mieux, à une vitesse moyenne de coureur d'ultrafond, on aura 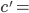c'= 6 km/h sur la distance d'un marathon, 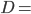42,195 km.

Les rôles sont alors inversés : c'est Kid Flash qui va pouvoir narguer ce molasson de Neutron.

On considère que le processus prend lorsque la distance restant à parcourir par Jimmy devient inférieure à 1 mètre.

Question 1 : au bout de combien d'allers-retours de Kid Flash le processus prend-il fin ?

Question 2 : quelle est alors la distance qu'il a parcourue ?

Notes

je laisse le soin aux lecteurs de le démontrer par récurrence, c'est trivial ↩
c'est valable sous l'hypothèse que j'ai rappelé dans ma remarque au début de l'article. ↩
idem, je laisse le soin aux lecteurs de le vérifier, c'est trivial... ↩
voir cet article sur techno-science.net : suite arithmético-géométrique. ↩
c'est trivial... ↩
c'est... presque trivial... ↩

Magazine Science