Histoire d’impédance

On entend souvent parler de résistances, mais dès qu’on farfouille un peu un drôle de terme, “impédance” nous poursuit. De quoi s’agit-il ?

Sans même connaître la loi d’Ohm, qui établit la proportionnalité entre tension et intensité dans un circuit électrique, nous sommes familiers avec le terme de résistance. Car qui n’a jamais bricolé étant enfant ces petits machins de toutes les couleurs ? Peut-être pas les filles… encore qu’il s’agisse sûrement d’un cliché !

Des résistances

L’unité de résistance est le ohm. Un ohm se définit comme la résistance électrique entre deux points d’un conducteur lorsqu’une différence de potentiel constante de 1 volt, appliquée entre ces deux points, produit dans ce conducteur un courant de 1 ampère, ledit conducteur n’étant le siège d’aucune force électromotrice (comprendre par là qu’on a affaire à un récepteur et non un générateur).

La résistance, c’est trop facile !

Intuitivement, la résistance est la difficulté de passage du courant : certains récepteurs, pour ne pas dire tous, laissent plus ou moins passer le courant. On a coutume d’utiliser l’analogie hydraulique : le courant électrique correspond au courant d’un fleuve (débit de charges électriques en fait) ; dans ce cas la résistance est l’écluse ! La résistance n’est donc pas un concept bien sorcier…

Or, qu’on soit un fana de physique ou un amateur de musique, on n’a pas souvent affaire à la résistance, mais à une autre notion : l’impédance. Lorsqu’on achète un amplificateur, une sono, un casque ou ne sais-je quel autre accessoire hi-tech, il est mentionné une impédance. Mais de quoi s’agit-il donc, si ce n’est que ça a un rapport avec la résistance…

U=ZI

En termes d’impédance, la loi d’Ohm s’écrit U=ZI : Z remplace R, pour la bonne raison que l’impédance est l’analogue de la résistance dans un circuit soumis à un courant alternatif sinusoïdal. Et pour cause : les courants continus étudiés au lycée ne sont pas monnaie courante. Le courant délivré au secteur est en effet alternatif, c’est-à-dire qu’il oscille, de même qu’un fleuve ferait des vagues, et ne coulerait pas avec un débit constant.

Impédance vient du terme anglais impede signifiant “faire obstacle à” : l’impédance fait obstacle au passage du courant alternatif, de même que la résistance s’oppose au courant continu. On l’utilise en médecine dans les examens d’impédancemétrie, où elle permet de définir la composition corporelle en fonction de l’atténuation d’un signal appliqué.

Esprits non téméraires, je vous conseille de vous arrêter ici, à moins que (niveau Terminale S) vous ne préfériez vous enfoncer dans les méandres passionnants de l’électronique !

Gare aux complexes

En toute rigueur, il convient de faire une autre différence entre impédance et résistance : la résistance est une grandeur réelle, alors que l’impédance fait appel aux nombres complexes. Comportant une composante imaginaire, elle est donc plus difficile à appréhender, mais pas impossible !

L’impédance est la propriété du circuit électrique à s’opposer au passage du courant alternatif à partir du moment où l’on combine des éléments possédant une réactance (condensateurs, inductances) et une résistance.

La réactance est simplement la partie imaginaire de l’impédance.

De même que la conductance est l’inverse de la résistance, l’admittance est l’inverse de l’impédance. La division étant une loi de composition interne dans le corps des nombres complexes, l’inverse d’un nombre complexe est également un nombre complexe !

La conductance est la partie réelle de l’admittance, tandis que la susceptance en est la partie imaginaire. Tout ce joyeux monde se mesure en siemens.

Finalement, la résistance n’est que la partie réelle d’un concept plus vaste : l’impédance. Du coup il est logique de retrouver la conductance en tant que partie réelle de l’inverse d’une impédance, donc d’une admittance. Le tout est de ne pas se mélanger les pinceaux ! En courant continu, seule la résistance importe, mais en courant alternatif on doit prendre en compte la partie imaginaire.

En fait, l’impédance d’une résistance est réelle : elle n’est autre que la résistance. Une résistance n’induit aucun déphasage du signal y transitant.

Concernant les lois d’additivité d’impédance, elles sont les mêmes que pour une résistance : dans un circuit série, les impédances s’ajoutent, tandis qu’en dérivation les admittances (et non plus les conductances) s’ajoutent.

Rien de plus à savoir sur le sujet… si ce n’est qu’on apprécie jouer avec les arguments et les modules

On travaille souvent en représentation de Fresnel, ce qui permet d’ajouter, soustraire, dériver ou intégrer des fonctions sinusoïdales de même fréquence, et ce en toute simplicité.

L’idée est la suivante : passer des chiffres aux repères. Les nombres complexes s’y prêtent aisément, au sens où leur partie réelle est l’abscisse, et leur partie imaginaire l’ordonnée. Mathématiquement, rien de plus simple que d’associer un vecteur à un nombre complexe ! Au nombre complexe a+i*b correspond le vecteur (a, b)…

De la sorte, si nous disposions d’un nombre complexe, ou mieux

Rappelons qu’à tout signal sinusoïdal correspond une fonction f telle que pour tout t positif ou nul :

f(t)=A*sin(ω*t+ϕ)

- A est l’amplitude du signal
- ω est la pulsation, terme barbare qui n’est rien d’autre que le produit de la fréquence par 2 π.
- ϕ est la phase à l’origine des dates (à t=0, quoi…)

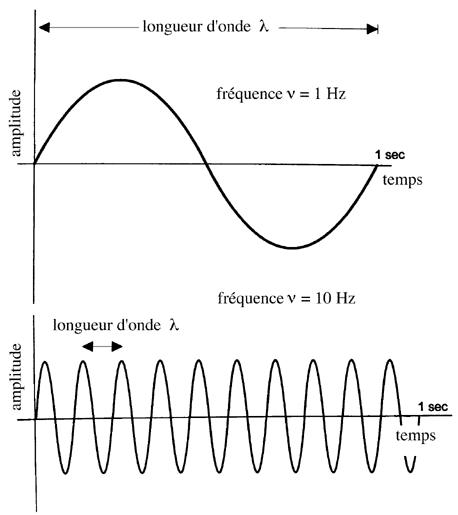
La fréquence, inverse de la période (durée d’un motif élémentaire), désigne le nombres de motifs par seconde. Elle est donc homogène à l’inverse d’une durée, et s’exprime en hertz.

Via la décomposition en séries de Fourier, tout signal peut d’ailleurs s’exprimer comme une somme de sinusoïdes, mais revenons-en à notre vecteur de Fresnel, nombre complexe incarné. Dans le plan, il aura pour module l’amplitude, et pour argument (donc angle polaire) la phase à l’origine. L’amplitude représente la valeur maximale pour les courants et les tensions ; cela dit on a pour habitude de jongler avec la la valeur efficace : il suffit d’appliquer un facteur racine de 2 pour s’y ramener.

Le rapport U/I des valeurs efficaces de la tension et de l’intensité est donc appelé impédance : il ne dépend que de la fréquence. Contrairement à une résistance, qui a toujours le même comportement vis-à-vis du courant, une impédance se comporte différemment selon la fréquence du courant qui la traverse. C’est un peu comme un grillage : on peut faire passer une balle de tennis à travers mais à condition d’aller lentement, si on la jette comme une brute elle risque d’être arrêtée. Bref, une impédance se comporte comme un filtre fréquentiel, ne laissant passer que certains courants, à certaines fréquences. Cette remarque capitale est à garder en tête pour la suite.

Le truc, c’est qu’on ne travaille pas avec les nombres complexe sous forme algébrique, ni même trigonométrique, mais sous forme exponentielle. S’y ramener étant un jeu d’enfant, voici un exemple :

soit un circuit RC série soumis à une tension e(t)=E*cos(ω*t+ϕ). On cherche à déterminer I. On aimerait bien appliquer la loi d’Ohm, mais c’est un peu (beaucoup) difficile :/

A couvert de réels…

Dieu soit loué, les nombres complexes dégainent leur revolver. Désormais, tensions et intensités auront également une composante complexe. Petite convention en physique, pour ne pas confondre le nombre imaginaire avec l’intensité, on le note j. Ce “j” n’en demeure pas moins le seul, l’unique, dont le carré vaut -1 (bon d’accord, y’en a un deuxième…) !

La fonction donnée, e(t) est une fonction réelle : elle n’est que la partie émergée de l’iceberg : une fonction complexe (en se rappelant que : A*e^i*x=A(cos(x)+i*sin(x)) – passage de la forme trigonométrique à exponentielle – et en distribuant, ainsi qu’en remplaçant x par ω*t, on a vite fait de le retrouver) !

Qu’elle n’est pas la joie de mettre la main sur cette fonction complexe : la voici, sur le tapis rouge, en petite tenue :

e(t)=U*e^j*ω*t

Un paparazzi me souffle qu’en physique le soulignement dénote la qualité complexe ! Loin d’être décomplexée, e(t) soulignée est une fonction complexe dont e(t) ne représente que la partie réelle.

D’après la définition de l’impédance, Z=R+j*X, où R est la résistance et X la réactance, ce qui s’écrit encore Z*cos(ω)+j*Z*sin(ω). On peut très bien factoriser par Z (module de l’impédance), mais cette notation a le mérite de présenter clairement deux termes importants :
-Z*cos(ω) : la résistance (partie réelle de l’impédance)
- Z*sin(ω) : la réactance (partie imaginaire de l’impédance)

Reprenons où nous en étions :

- La tension complexe aux bornes de la résistance s’écrit : u_R(t)=U_C*e^j*ω*t

- La tension complexe aux bornes du condensateur s’écrit : u_C(t)=U_Re^j*ω*t

- Comme on est dans un circuit série, l’intensité est la même en tout point. L’écriture complexe de cette intensité est : i(t)=I*e^j*ω*t.

D’après la loi des mailles, U_C+U_R=ZI.
L’impédance, elle, est tout bêtement la somme des impédances (circuit série) : Z= Z_C+Z_R. L’impédance d’une résistance se confond avec la résistance, quant à l’impédance d’un condensateur, elle est à apprendre :

L’impédance d’un condensateur vaut -j/Cω (avec C la capacité du condensateur, en farads).

Remarquez au passage que si je ne prends pas la peine de souligner les Z, alors qu’il s’agit de valeurs complexes (de toute manière, même les réels sont des complexes de partie imaginaire nulle !), c’est parce qu’en parlant d’impédance, tout le monde comprend bien qu’il s’agit d’une caractéristique complexe.

Du coup, notre équation se pare de ses plus beaux atours : Z=R-j/Cω. Reste à appliquer la loi d’Ohm pour trouver I !

En représentation de Fresnel, l’ordonnée (axe imaginaire) figure la réactance, tandis que l’abscisse (axe réel) figure la résistance. Par le théorème de Pythagore, l’amplitude, module de la fonction complexe et norme du vecteur, est la racine de la somme des carrés de la réactance et de la résistance.

Nous le savons fort bien à cause du cercle trigonométrique définissant les fonctions sinus et cosinus : la projection d’un vecteur sur un axe définit une fonction sinusoïdale.

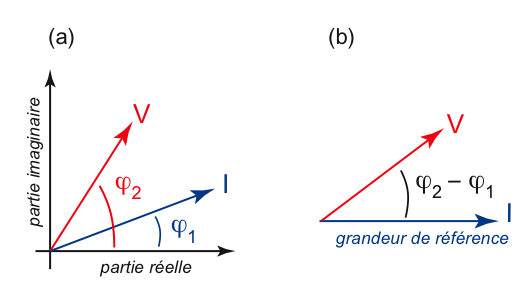
La représentation de Fresnel permet de s’affranchir des calculs avec les nombres complexes.

Reste à préciser que le couple (module, argument) est caractéristique d’un dipôle en régime sinusoïdal.

Un dipôle dont le courant et la tension sont en phase est dit résistif : il se comporte comme une résistance pure. Dans la représentation de Fresnel, les vecteurs courant et tension sont colinéaires, étant donnée la synchronicité (même phase, même argument, je n’oserai pas dire même combat pour lutter contre le courant !).

Tout l’intérêt de la représentation de Fresnel est par exemple qu’elle permet d’ajouter visuellement deux signaux sinusoïdaux d’amplitude différente : il n’y a qu’à calculer le vecteur-résultante.

Les filtres, les filtres !

Dans l’hypothèse hautement improbable où un novice serait parvenu jusqu’ici, une question ne lui échapperait pas : à quoi ça sert tout ça ? C’est bien joli les impédances, mais ça ne mange pas en salade…

En fait, les impédances ne servent pas à grand chose, si ce n’est à téléphoner, écouter la radio, recevoir la télévision, surfer sur Internet, et toutes sortes de télétransmissions ! Les impédances sont à la base de notre civilisation, car elles servent dans les filtres fréquentiels.

En effet, comment fonctionne un tuner radio ? L’appareil baigne dans un flot d’ondes-radio, modulées en fréquence (FM) ou en amplitude (AM) afin de porter une information ; reste à tourner le molette pour sélectionner le bon canal. En jouant avec les ondes sinusoïdales, on se branche littéralement sur la bonne station.

L’idée

L’idée, toute simple, consiste à se remémorer une remarque du début : selon l’impédance utilisée, il y a possibilité de laisser passer ou non certains signaux. En jouant sur l’impédance, on filtre les signaux !

Fonctionnement d’un filtre du premier ordre

Je n’évoque ici que les filtres dits linéaires du premier ordre, dont la réponse est proportionnelle à l’excitation : vous vous doutez bien qu’il existe des filtres ultra-sophistiqués pour téléphoner sur la Lune (par exemple !)…

Un filtre simple se compose d’une seule résistance-réactance, bref… d’une impédance !

La notion-clé à maîtriser pour comprendre le phénomène est la fonction de transfert. Il s’agit du rapport des tensions complexes sortie/entrée. On parle de filtre linéaire bel et bien en raison d’une relation de proportionnalité entre la tension d’entrée et celle en sortie :

V_sortie/V_entrée=H(jω)

H(jω) est la fonction de transfert ; plus qu’une constante de proportionnalité, c’est une fonction de la pulsation imposée par le générateur (ω), donc de la fréquence du courant alternatif. Le filtre traite ainsi le signal d’entrée, en l’amplifiant d’un certain facteur (pas nécessairement positif, mais une atténuation de signal n’est rien d’autre qu’une amplification négative !). Ce facteur, primordial dans l’étude d’un filtre, est égal au module de la fonction transfert. On l’appelle gain et on note G :

G=|H(jω)|

Par souci de clarté, on utilise plutôt une échelle logarithmique, en décibels :

G_dB=20*log(H)

Quant au déphasage du signal entre l’entrée et la sortie du filtre, c’est un argument de la fonction de transfert.

Un exemple : le filtre passe-bas

Considérons le circuit RC ci-dessous :

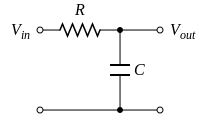
La formule du diviseur de tension permet d’établir la relation entre tension de sortie et tension d’entrée :

Ainsi, la fonction de transfert de ce filtre, rapport sortie/entrée, est

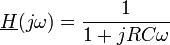
Une limite

La perle des remarques, c’est celle-ci : la fonction de transfert tend vers 0 lorsque la pulsation, donc la fréquence, devient grande. Par conséquent (transfert nul), les hautes fréquences ne sont pas transmises. Le filtre est dit passe-bas : il laisse passer seulement les signaux basse-fréquence.

Petite remarque

RC est homogène à un temps (c’est la constante de temps du circuit RC). Donc la quantité 

 est homogène à une pulsation : elle est appelée pulsation propre du système.

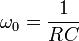
On peut donc réécrire la fonction de transfert :

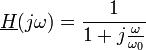
Filtres passe-haut et passe-bande

Par un raisonnement similaire, les filtres ne laissant passer que les hautes fréquences sont dit passe-haut.

Enfin, certains filtrent ne laissent passer qu’une plage de fréquences (par laisser passer, on entend ne pas amortir le signal).

Du coup, le principe de la radio (du moins pour sa partie tuner) est simple : avec une molette combinée à un ingénieux système d’engrenages, on règle le calibrage de filtres pour écouter une certaine fréquence. Grâce à la FM (modulation de fréquence), les signaux reçus portent une information qu’il ne reste plus qu’à démoduler puis à restituer grâce à un haut-parleur !

Bien que cette technologie analogique soit supplantée par le numérique, elle a le mérite d’illustrer simplement la sélection des signaux électriques, donc électromagnétiques grâce aux antennes chargées de la conversion. Dans le cas d’un récepteur-radio, sélectionner un signal électrique particulier revient donc à “écouter” une portion définie du spectre électromagnétique.

Facteur de qualité

Pour juger de la qualité d’un filtre, on utilise le facteur de qualité, qui est une mesure du taux d’amortissement de l’oscillateur. A la résonnance, l’impédance d’un circuit est minimale : mieux vaut ne pas trop s’opposer aux oscillations ! Le signal transmis est alors maximum.

Q est le rapport de la fréquence propre (quotient de la pulsation propre par 2 π) à la largeur de la bande passante à la résonance.

Plus le facteur de qualité est élevé, plus le filtre est sélectif. Llogique : les bonnes vieilles radios peinent à faire la différence entre 97.8 et 97.9 MHz. La qualité est, entre autres, une affaire de sélectivité : un éméteur agissant sur la voiture télécommandée du voisin n’est pas des meilleurs !

Ce facteur de qualité ne tombe pas du ciel en parachute… On le retrouve aisément dans l’équation différentielle régissant l’évolution du système, à condition de la mettre sous forme canonique. Elle vaut ω₀*τ, avec ω₀ la pulsation propre, et τ la constante de temps, trouvable dans l’équation différentielle.

Dans un circuit RLC série, par exemple, le facteur de qualité s’exprime ainsi :

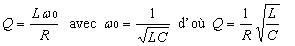
Il découle de l’équation différentielle obtenue par loi des mailles de Kirchoff :

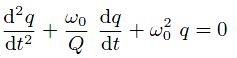
Le facteur de qualité est utile. En particulier, dans un circuit RLC série soumis à un échelon montant de tension, on distingue trois cas (correspondant à la valeur respectivement positive, nulle, ou négative du discriminant associé au polynôme caractéristique de l’équation différentielle du second ordre) :

- Q<1/2 : régime apériodique
- Q=1/2 : régime critique
- Q>1/2 : régime pseudopériodique

Bande passante à -3 dB

On appelle fréquence de coupure la fréquence pour laquelle le gain vaut -3 dB.

Dans le cas d’un filtre passe-haut, il existe une fréquence coupure basse.
Dans le cas d’un filtre passe-bas, il existe une fréquence coupure autre.
Dans le cas d’un filtre passe-bande, il existe deux fréquences de coupure : une haute et une basse.

La bande passante est l’ensemble des fréquences passant sans atténuation, c’est-à-dire qu’un filtre coupe les signaux hors bande passante. Elle est constituée des fréquences pour lesquelles le gain (en décibels) est supérieur au gain maximal moins 3 décibels.

Dit autrement, la bande passante est l’intervalle [fréquence coupure basse, fréquence de coupure haute] tel que G_dB≥G_{dB, max}-3.

D’autres définitions que la bande passante à -3 dB sont possibles, mais c’est la plus courante ! Pour information, si on ne raisonne pas en décibels, cette bande correspond à la plage de fréquences où le gain est supérieur au gain maximum divisé par racine de deux.

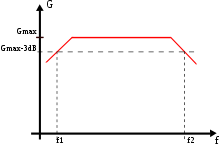
La zone en rouge représente le signal, et l’intervalle [f1, f2)] la bande passante à -3 dB.

Diagramme de Bode

Pour analyser la réponse en fréquence d’un dispositif, on se sert d’un diagramme de Bode. Quand a bien compris le gain en décibels, c’est plus simple qu’il n’y paraît !

Un diagramme de Bode est un diagramme présentant simultanément le gain et la phase en fonction de la pulsation (donc de la fréquence). Seule particularité : une échelle logarithmique est utilisée en abscisse, en raison de la large gamme de pulsations : il faudrait une bien large feuille avec une échelle linéaire, c’est pourquoi on se sert de papier semi-logarithmique.

Un diagramme de Bode indique donc comment se comporte un circuit au fur et à mesure que varie la fréquence. Le diagramme se compose de deux sous-diagrammes :

- Le diagramme de phase

- Le diagramme de gain

Comme nous l’avons vu, le gain correspond au module de la fonction de transfert, et le déphasage à un argument. Connaissait ces données, il n’y a plus qu’à tracer les deux courbes !

Pour cela, on cherche le comportement du gain et de la phase aux extrêmes de la bande fréquentielle applicable au circuit, c’est-à-dire lorsque f → 0 et f → +∞. Nous n’aurons ainsi qu’à tracer les asymptotes pour effectuer un tracé grossier !

Il est bon de figurer les pentes et les limites :

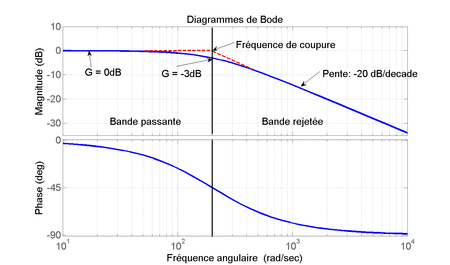
Diagramme de Bode d’un filtre passe-bas. L magnitude n’est autre que le gain : c’est une allusion à l’échelle logarithmique des bels, de même qu’on parle de magnitude d’un séisme !

L’amplificateur opérationnel

Que serait un appareil électronique sans ampli-op ? L’amplificateur opérationnel est un circuit intégré qui, dans la même veine que les filtres, traite le signal en amplifiant une différence de potentiel appliquée à ses bornes. A la différences des dipôles, il s’agit d’un quadripôle : deux entrées (reliées à un générateur) – l’une dite inverseuse (+), et l’autre non-inverseuse (-) – deux sorties (reliées à un circuit d’utilisation).

La bête, c’est lui : l’amplificateur opérationnel !

L’amplificateur opérationnel est aujourd’hui dépassé avec les technologies numériques, mais n’en reste pas moins encore très présent. Mis au point dans les années 1960, il fit son apparition sur le marché dans les années 70. L’ampli-op est doté d’une remarquable aptitude à l’amplification de signal, mais il permet aussi de faire des opérations sur les signaux.

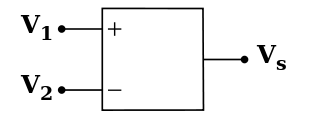
Schéma européen d’un amplificateur opérationnel (la sortie reliée à la masse n’est pas représentée). Comme toute impédance, on peut, selon le montage, lui associer une fonction de transfert.

On peut le brancher en amplificateur inverseur, non-inverseur, comparateur ou en montage suiveur, mais aussi le brochage permet l’addition, la soustraction, la dérivation, l’intégration, l’exponentiation, ou la “logarithmation” (!) de signaux.

La différence de potentiel entre les deux entrées est appelée tension offset. Dans l’hypothèse où l’impédance d’entrée est infinie, aucun courant ne circule entre les deux entrées.

Voilà donc, sommairement, pour les impédances et leur utilisation !

Petit conseil, ne pas trop chercher à se représenter ce que sont des grandeurs complexes ! La notation complexe ne fait que simplifier les choses ; c’est un outil mathématique pour éviter d’avoir à en découdre avec des équations différentielles ! Bien entendu, on a une pomme ou deux dans son panier, et cette phrase à méditer : la raison pour laquelle la vie est complexe est qu’elle comporte une partie réelle et une partie imaginaire.

48.856667 2.350987