Production de la mesure de value at risk (VaR)

Cette article fait partie d'une série d'article sur les mesures de risque financier: Introduction à la VaR, EEPE et la CVA.
Cet article doit beaucoup à l'ouvrage de risque financier de Glynn A. Holton, Value-at-Risk: Theory and Practice.

Value at risk: une formalisation

Toute mesure de risque doit mesurer deux paramètres distincts: une exposition et un degré d'incertitude qui reflète une distribution de probabilité des événements adverses affectant un portefeuille. Par ailleurs, cette mesure est toujours associée à un horizon de temps T. T prend couramment la valeur 1 an ou 1 jour. Dans le cas de la VaR, le degré d'incertitude est fixé: on parle de VaR à 99% ou 95%.
Dans le cas le plus simple, on peut construire une mesure de la VaR aisément.Il faut pour cela faire l’hypothèse d'une distribution de probabilité suivant loi normale normée centrée réduite. Dans ce cas, il suffit seulement de calculer l’écart type σ sur la période concernée (par exemple 1 an ou 1 jour), on a alors:
VaR=σ_T.N^-1(X)
ou
X est le degré de certitude associé à la mesure de VaR
N^-1 est la loi normale cumulative inversée
σ_T est l'écart type calculé  sur la période [0;T]
Mais dans le cas général, cette approximation ne permet pas de modéliser correctement les fluctuations d'un portefeuille complexe de dérivés. On est donc obligé de mettre en place une procédure pour déterminer une distribution de probabilité des événements adverses affectant le portefeuille. Il y de nombreuses façon de construire cette distribution, que nous allons détailler, mais pour l'associer à une mesure, il est nécessaire de pouvoir construire une métrique. Dans le cas de la VaR, la métrique qui s'applique à la distribution de probabilité est la l'estimateur par quantile.

Caractérisation de l'estimateur par quantile

Cette section suit les notations du cours de Peter Haas sur l'estimation des quantiles
Notons X la variable aléatoire réelle représentant les pertes d'un portefeuille. Sa fonction de répartition F_X est inconnue. Nous définissons une probabilité p par exemple 0.01% correspondant à notre degré de certitude, la VaR est lié correspond au montant négatif q des pertes tel que : Pr(X<q)=p par définition de la fonction de répartition, on a F_X(q)=P soit  q_p=F_X^-1(p).Comme la F_X est inconnue, ou n'accepte pas de forme analytique, nous introduisons l’estimateur statistique,  Q_n=F_n^-1 (p) tel que: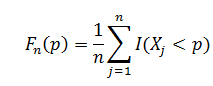Ou X₁, X₂,...,X_n sont des variables indépendantes et identiquement distribuées. Une façon équivalente de définir  cet estimateur est par un ordonnancement des X_i précédents. Soit  X₍₁₎, X₍₂₎,...,X_(n) les valeurs telles que X₍₁₎≤ X₍₂₎≤...≤X_(n) , on a :
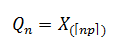Q_n est la np eme plus petite réalisation de X_i.
La convergence de cet estimateur est garantie par le théorème central limite. Il faut noter toutefois que le degré d'erreur de l'estimateur est dépendant de la "normalité" de la distribution. Plus la distribution exhibe des caractéristiques non normale, à savoir Kurtosis et asymétrie (skewness), plus le degré d'erreur est important. Notons qu'un autre estimateur recommandée par le comité de Bale III, l'expected shortfall est plus résilient dans le cas général pour les distributions présentant des "fat tails".
On notera que la convergence de cette estimateur introduit un degré d'erreur qui est inversement proportionnel à la racine de n et proportionnel à la variance de X. De sorte que si on augmente le nombre d'observations par 4, on on observe une amélioration de l'estimation par un facteur de 2...

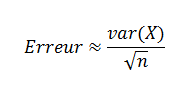
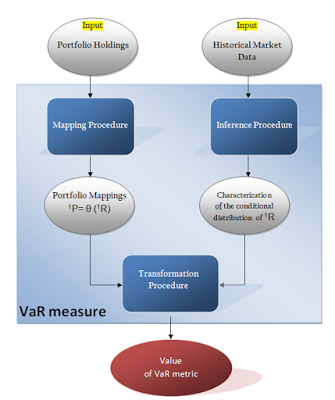
Notre Framework de calcul de la VaR

Nous allons considérer le calcul d'une VaR à un horizon T. Ce mécanisme peut aisément être adapté à n pas de temps t₁,...,t_n. En ne considérant qu'un intervalle de temps, on notera t₀ la date initiale de notre intervalle et t₁ la fin de notre horizon de temps.
On notera ⁰P,¹P la valeur de notre portefeuille respectivement à t₀ et t₁. On notera ¹L le montant des pertes en t₁. on a  ¹L=⁰P-¹P. Au début de la simulation seul ⁰P est connu avec certitude.
La VaR que nous souhaitons obtenir sera un quantile choisi de la distribution de  ¹L sur notre horizon de temps.
Pour calculer la valeur de notre portefeuille, nous allons le diviser en k actifs de valeurs (S_i)_0≤i≤k. Ces actifs vont fluctuer entre 0 et 1 de la maniére suivante:

Il faut ensuite décomposer notre portefeuille en holdings: le décomposer comme une somme d'actifs. Par exemple, si notre portefeuille détient ω_i titre de l'actif S_i, la valeur de ces titres pour le portefeuille sera ω_i.S_i.

Les  fluctuations de nos actifs sont liées à l'évolution de facteur clés, comme la valeur des taux, la credit curve, les taux de changes, les volatilités, etc.... On notera ⁰R et ¹R le vecteur des Q facteurs d’évaluation des actifs respectivement au début de la période et à la fin de l'horizon de temps:
On notera que le vecteur ¹R est obtenu par un processus d'inférence statistique (voir schéma en tête de notre article). L'inférence statistique est ici utilisée pour déduire les valeurs des facteurs clé de notre VaR à la fin de l'horizon de temps considéré. Pour ce faire, il est nécessaire de collecter le plus d'observations possibles des valeurs historiques de marché de ces facteurs.  Soit ^-ir_j une observation historique au i eme jour précédent notre calcul pour le facteur clé j. Les vecteurs ^-1r,^-2r,...,^-Nr sont utilisés pour inférer notre ¹R.
Ces vecteur peuvent être utilisée pour une inférence historique simple, ou Ils peuvent être utilisés pour calibrer un modèle de diffusion statistique, par exemple un modèle de taux.
Pour chaque actif S_i, on peut déterminer une fonction de pricing Φ_i dépendante des facteurs clé qui vérifiera la relation suivante:
S_i= Φ_i(¹R)
De notre que notre valeur de portefeuille sera exprimée par:
¹P=ω₁.Φ₁(¹R)+ω₂.Φ₂(¹R)+...+ω_p.Φ_p(¹R)soit¹P= Θ( ¹R)
La construction de cette expression de la valeur du portfolio est appelée le mapping Θ. Souvent pour des produits complexes, il n'est pas possible de construire un Θ exact. Il est nécessaire de construire une valeur de Θ approximée. cette approche est appelée un remapping. Il est possible de construire de mappings linéaires ou quadratiques de simplification par exemple (voir Glynn A. Holton, Value-at-Risk: Theory and Practice).
La dernière étape de ce processus est la Transformation.

La transformation de monte carlo

Le mapping et l'inférence que nous avons évoqués ci dessus permettent de construire la valeur future de notre portefeuille et donc les pertes éventuelles associées, mais elle ne permet pas de construire une distribution de probabilité des pertes a l'Horizon T. Or par définition, la VaR est une mesure par quantile qui nécessite une vision statistique.
Pour construire cette distribution des pertes de notre portefeuille, on peut soit proposer une modélisation de cette distribution (normale, quadaratique) soit essayer de la construire par construction de réalisation statistiques (sampling). Cette méthode est appelée méthode de Monte Carlo.
Dans la pratique, il s'agit de construire N réalisations conjointe de nos facteurs clés, et d'évaluer la valeur du portefeuille pour chacune de ces réalisations. Cette opération nécessite d'avoir un nombre de réalisation N important pour réduire l’erreur associée à ce processus. Mais évaluer N fois un portefeuille est un traitement couteux en terme de temps de traitement, il convient donc de trouver un arbitrage entre précision et temps de calcul.
Par ailleurs, il faut noter si l'évaluation par Monte Carlo est beaucoup plus efficiente quand le nombre de paramètres probabiliste dépasse 3. En effet, la complexité de la méthode de monte carlo augmente linéairement avec le nombre de paramètres alors que d'autres méthodes croissent de manière exponentielle.

Formalisation

Supposons que nous avons un couple (⁰P,¹P) construit avec le mapping ¹P = θ(¹R). Nous pouvons construire par sampling m valeurs de notre vecteur de facteurs {¹R^[1], ¹R^[2], … , ¹R^[m]}. Ceci génère m valeurs du portefeuille {¹P^[1], ¹P^[2], … , ¹P^[m]} car on peut définir ¹P^[k] = θ(¹R^[k]).
Pour construire m réalisation de notre vecteur de facteur clés, il existe deux approches distinctes:

• La méthode historique (et historique adaptée)
• La méthode aléatoire (Pseudo random vectors)

La description de ces méthodes est hors du scope de cet article de blog. Un dernier point doit être toutefois précisé.
Pour la méthode historique, il est courant d'adapter  les résultats obtenus en ajoutant un bruit blanc. Dans ce contexte, la simulation n'est ni totalement historique ni totalement paramétrique.

Annexes

Why risk is so hard to measure
Jon Danielson & Chen Zhou
Quantile Estimation
Peter J. Haas
Glynn A. Holton, Value-at-Risk: Theory and Practice