Un 45ème nombre de Mersenne premier peut-être découvert

Un nombre premier est un nombre divisible par 1 et par lui-même, comme 3, 5 , 7....

Un nombre de Mersenne est un nombre entier de la forme :

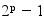
Les nombres de Mersenne fournissent de bons candidats pour les nombres premiers, à condition que p soit premier

Par exemple pour p=3, le nombre de Mersenne vaut

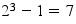
et il est premier.
Mais pour p=11, le nombre de Mersenne vaut

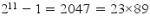
et n'est pas premier.

En fait, l'humanité n'a pour l'instant trouvé "que" 44 nombres premiers de Mersenne, leur avantage étant qu'ils produisent les plus grands nombres premiers connus. Voilà le tableau des nombres de Mersenne connus à ce jour. Le plus grand est colossal et possède 9 808 358 chiffres.

# p M_p Chiffres Découverte Découvreur

1 2 3 1 Antiquité Inconnu

2 3 7 1 Antiquité Inconnu

3 5 31 2 Antiquité Inconnu

4 7 127 3 Antiquité Inconnu

5 13 8 191 4 XIII^e siècle Ibn Fallus

6 17 131 071 6 1588 Cataldi

7 19 524 287 6 1588 Cataldi

8 31 2 147 483 647 10 1750 Euler

9 61 2 305 843 009 213 693 951 19 1883 Pervushin

10 89 618970019…449562111 27 1911 Powers

11 107 162259276…010288127 33 1914 Powers

12 127 170141183…884105727 39 1876 Lucas

13 521 686479766…115057151 157 30 janvier 1952 Robinson (Swac)

14 607 531137992…031728127 183 30 janvier 1952 Robinson (Swac)

15 1 279 104079321…168729087 386 25 juin 1952 Robinson (Swac)

16 2 203 147597991…697771007 664 7 octobre 1952 Robinson (Swac)

17 2 281 446087557…132836351 687 9 octobre 1952 Robinson (Swac)

18 3 217 259117086…909315071 969 8 septembre 1957 Riesel (Besk)

19 4 253 190797007…350484991 1 281 3 novembre 1961 Hurwitz (IBM)

20 4 423 285542542…608580607 1 332 3 novembre 1961 Hurwitz (IBM)

21 9 689 478220278…225754111 2 917 11 mai 1963 Gillies (Illiac)

22 9 941 346088282…789463551 2 993 16 mai 1963 Gillies (Illiac)

23 11 213 281411201…696392191 3 376 2 juin 1963 Gillies (Illiac)

24 19 937 431542479…968041471 6 002 4 mars 1971 Tuckerman (IBM)

25 21 701 448679166…511882751 6 533 30 octobre 1978 Noll & Glenn (CDC)

26 23 209 402874115…779264511 6 987 9 février 1979 Noll (CDC)

27 44 497 854509824…011228671 13 395 8 avril 1979 Nelson & Slowinski (Cray Research)

28 86 243 536927995…433438207 25 962 25 septembre 1982 Slowinski (Cray)

29 110 503 521928313…465515007 33 265 28 janvier 1988 Colquitt & Welsh (Nec)

30 132 049 512740276…730061311 39 751 19 septembre 1983 Slowinski (Cray)

31 216 091 746093103…815528447 65 050 1 septembre 1985 Slowinski (Cray)

32 756 839 174135906…544677887 227 832 19 février 1992 Slowinski & Gage

33 859 433 129498125…500142591 258 716 10 janvier 1994 Slowinski & Gage

34 1 257 787 412245773…089366527 378 632 3 septembre 1996 Slowinski & Gage

35 1 398 269 814717564…451315711 420 921 13 novembre 1996 GIMPS / Joel Armengaud

36 2 976 221 623340076…729201151 895 932 24 août 1997 GIMPS / Gordon Spence

37 3 021 377 127411683…024694271 909 526 27 janvier 1998 GIMPS / Roland Clarkson

38 6 972 593 437075744…924193791 2 098 960 1^er juin 1999 GIMPS / Nayan Hajratwala

39 13 466 917 924947738…256259071 4 053 946 14 novembre 2001 GIMPS / Michael Cameron

40^* 20 996 011 125976895…855682047 6 320 430 17 novembre 2003 GIMPS / Michael Shafer

41^* 24 036 583 299410429…733969407 7 235 733 15 mai 2004 GIMPS / Josh Findley

42^* 25 964 951 122164630…577077247 7 816 230 18 février 2005 GIMPS / Martin Nowak

43^* 30 402 457 315416475…652943871 9 152 052 15 décembre 2005 GIMPS/ Cooper & Boone

44^* 32 582 657 124575026…053967871 9 808 358 4 septembre 2006 GIMPS/ Cooper & Boone

Lorsque l'exposant p commence à devenir important, il est nécessaire d'avoir recours à l'ordinateur, et même d'utiliser plusieurs ordinateurs. C'est ce que fait le projet GIMPS depuis 1996 où l'on constate dans le tableau précédent que ce mode de calcul a permis de découvrir les 10 derniers nombres premiers de Mersenne et donc les plus grands nombres premiers connus à ce jour.

Il semblerait qu'un 45ème nombre de Mersenne ait été découvert par GIMPS.

Mon ordinateur est associé à ce projet. par exemple en ce moment, mon ordinateur teste le nombre M39760033. C'est peut-être grâce à moi qu'a été découvert un 45ème nombre premier, ce 23 août. Si c'est le cas, j'espère qu'une partie des $100 000 de récompense me reviendra mais j'ai comme un doute...

En plus le propriétaire était en vacance ( pas moi ) celui de GIMPS... donc la validation du résultat devra attendre la mi-septembre.

On August 23rd, a computer reported finding a new Mersenne prime to the server! Because I was on vacation, verification did not begin until the 26th. Two verification runs are in progress. Estimated completion is September 12th and September 16th. Check back here for updates!

L'article de Scientific American:

World record ($100,000) prime number found?