Sine Qua Non est un traceur de courbes. Il est destiné spécialement aux professeurs de mathématiques de lycées, mais peut aussi être utilisé avec profit par les élèves.
Les principales caractéristiques sont les suivantes :
- La taille du dessin est réglable jusqu’à un maximum d’une page A4.
- L’orientation du document imprimé peut être paysage ou portrait.
- Le repère est entièrement paramétrable et peut être occulté.
- Les unités sont, par défaut, basées sur une grille à petits carreaux de 5x5 mm.
- Les unités du repère, les dimensions du dessin et des marges peuvent être définies au millimètre près.
- L’origine des axes du repère peut être quelconque (pas forcément 0).
- La syntaxe utilisée pour la saisie des fonctions est très proche de celle employée sur les calculatrices graphiques.
- L’utilisateur peut définir, sur un même dessin, jusqu’à 10 courbes représentant des fonctions, 10 courbes paramétrées et 10 courbes en coordonnées polaires.
- Sur chaque courbe, on peut représenter des points particuliers (tangentes, extrema…)
- Chaque courbe est définie par son équation (ou ses équations s’il s’agit d’une courbe paramétrée), son style (continu, pointillé ...), sa couleur et son épaisseur.
- Il est possible de définir des droites par leurs équations réduites.
- Les conventions habituelles de dessin sont respectées en ce qui concerne les extrémités des intervalles de définition.
- La composition des fonctions est possible.
- Les constantes p et e sont reconnues.
- Pour réaliser des schemas, l’utilisateur dispose d’une palette complète d’outils variés (points, segments, vecteurs, demi droites, polygones, cercles, angles, courbes de Bézier…)
- Il est possible également de faire des statistiques (1 ou 2 variables) et des probabilités (loi binômiale, loi de Poisson et loi de Gauss) et de visualiser les données sous forme de graphiques variés (histogrammes, boîtes à moustaches ...)
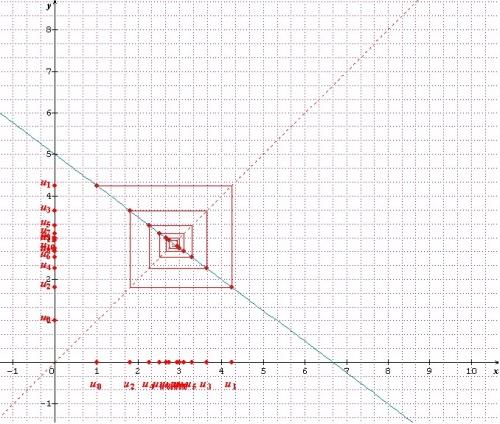
- On peut visualiser des suites numériques de type un=f(n) ou un=f(un-1) (escaliers ou spirales)
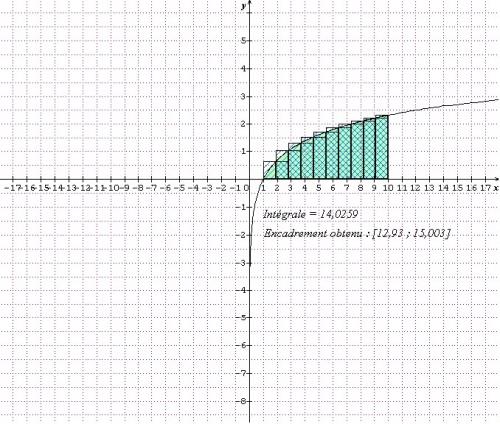
- On peut calculer et visualiser une intégrale en hachurant le domaine correspondant,
- Pour tracer une courbe point par point, on peut définir une liste de points par leurs coordonnées. Le logiciel propose alors 2 options : soit on indique la pente de la courbe en chaque point, soit on laisse le logiciel faire des interpolations par courbes de Bézier avec un coefficient de lissage paramétrable.
- Un nouveau menu permet de faire des calculs. Pour le moment, seule la fonction "résoudre une équation" est disponible (équivalent de la fonction "solve" des calculatrices). Cette commande permet de visualiser sur le graphique les différentes solutions d'une équation quelconque. D'autres commandes viendront par la suite.
- Le menu "calculs" s'enrichit d'une nouvelle commande : Table de valeurs.
- Nouvelle commande : systèmes d'inéquations à 2 inconnues.
- Calcul approché d'une intégrale par la méthode des rectangles ou des points-milieu ou des trapèzes.
- Ajout d'expressions mathématiques écrites en LaTeX sur le dessin (utilisation de MimeTex.dll écrite par John Forkosh sous licence GPL)
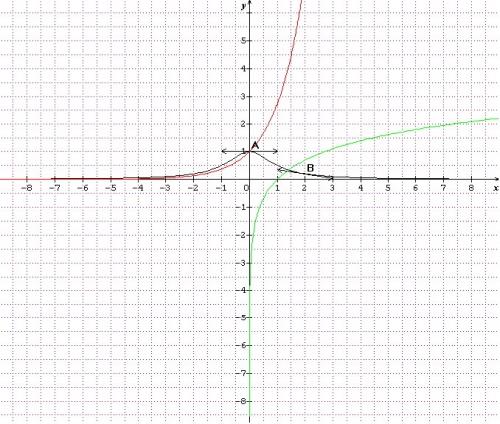
Voilà quelques exemples de tracés :