Des cellules qui se tiennent à carreau

Transcription de la chronique pour la 536ème émission de Podcast Science, dont la thématique était le carré.

Je vous en faisais la confession lors de ma chronique pour l’émission radio-dessinée “Science ou plaisir : pourquoi choisir?” : je suis un poil maniaque. Pas étonnant lorsque l’on sait qu’une grande partie de mon travail de laboratoire consiste à aligner et classer des séquences de protéines… Alors oui, c’est moi le gars en soirée que vous allez trouver en train de trier les M&Ms ou les confettis selon leurs couleurs. Je suis l’hurluberlu qui peut tailler des crayons pour qu’ils aient tous la même taille. Et enfin, oui, n’en déplaise à Robin qui doit trouver les étals de maraîcher merveilleux, je suis l’énergumène qui pense que les pommes, les tomates et les pamplemousses, c’est vraiment des fruits à la forme sub-optimale.

Quelle ne fut pas alors ma joie d’apprendre que certains fruits rentrent littéralement dans les cases, comme des pastèques carrées qui sont vendues régulièrement au japon, aux states et en allemagne. Leur prix est prohibitif et leur goût pas fameux, mais quel plaisir à ranger ! Il s’agirait de l’invention de l’artiste et horticulteur Tomoyuki Ono, inspiré par des productions du village de Zentsuji dans la province de Kagawa, qui aurait même déposé un brevet en 1977 ! En gros, on confine une pastèque en maturation dans un moule cubique.

Je vous laisserai dans les notes de l’émission un tutoriel pour faire pousser vos propres pastèques carrées (sachant que des version en forme de coeur, pyramide ou mickey existent aussi, compilées dans une magnifique page wikipédia intitulée Légume-phénomène).

Ce qui est un peu décevant, c’est qu’il s’agit ici d’un artifice pour rendre carrés des produits qui n’ont pas naturellement cette forme. Est-ce que des organismes carrés ça n’existe pas ? Malheureusement pour les fans de minecraft, ça ne se bouscule pas au portillon. On pourrait citer certaines étoiles de mer blessées qui prennent cette forme, mais c’est un peu de la triche…

Si on plisse les yeux, on pourrait accepter l’exemple de certains poissons-coffres, comme le bien nommé Ostracion cubicus, mais si on est honnête il faut admettre qu’il adopte plus une forme de rectangle tetrapak qu’un véritable cube…

C’est chez les microbes qu’on trouve les exemples les plus convaincants, notamment chez ceux du genre Haloquadratum. Décrits en 1980 comme des bactéries carrées, il s’agit en réalité d’organismes appartenant à un groupe frère appelé les archées et qui sont plus ou moins carrées.

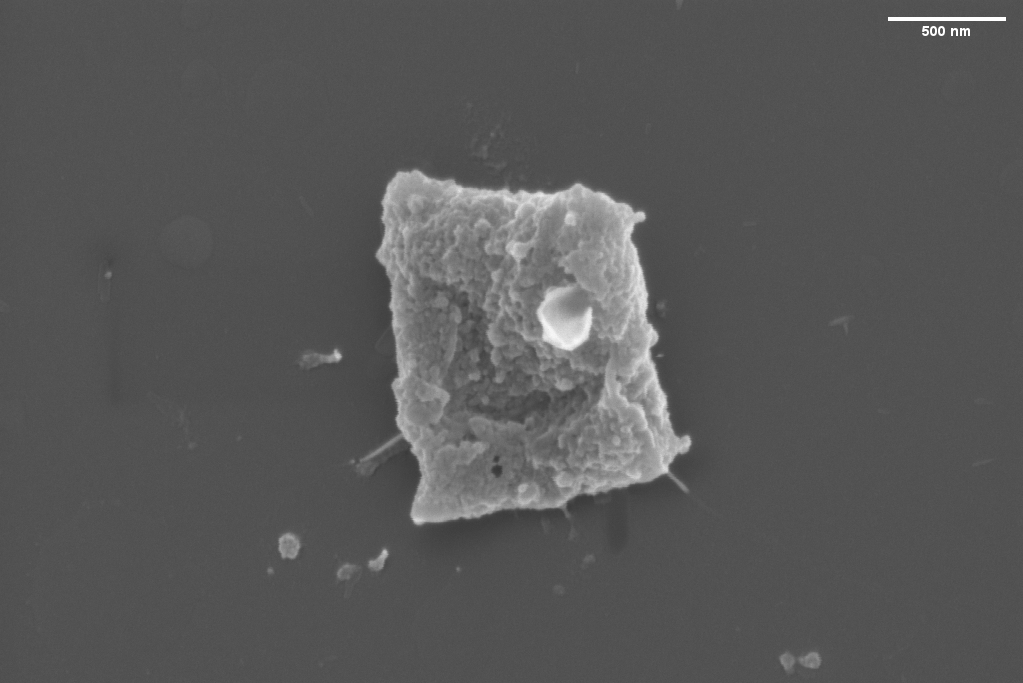
Mais selon moi, l’exemple le plus convaincant d’organisme carré est bel et bien une bactérie, appelé Candidatus Thiosymbion cuboideus.

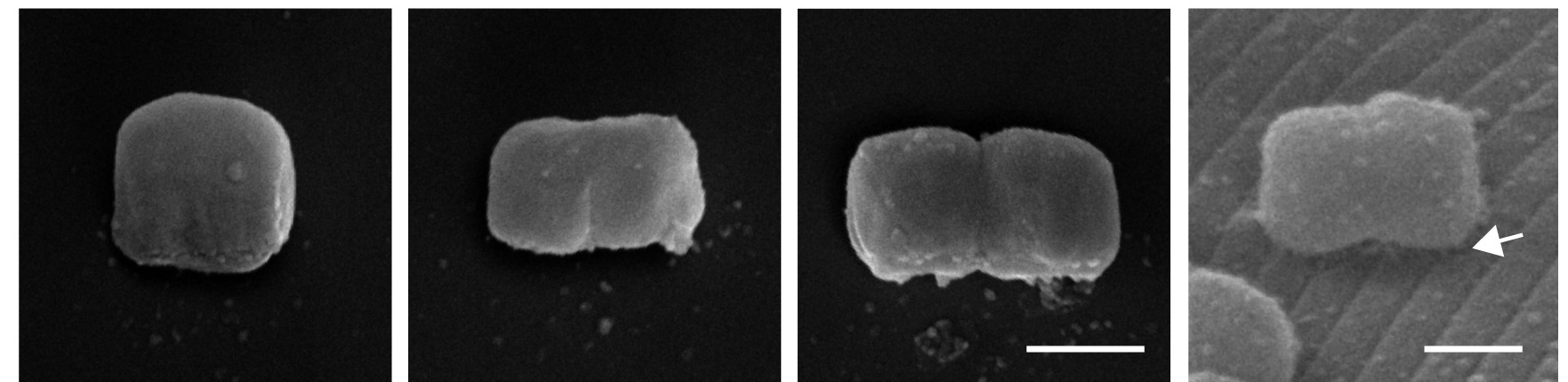
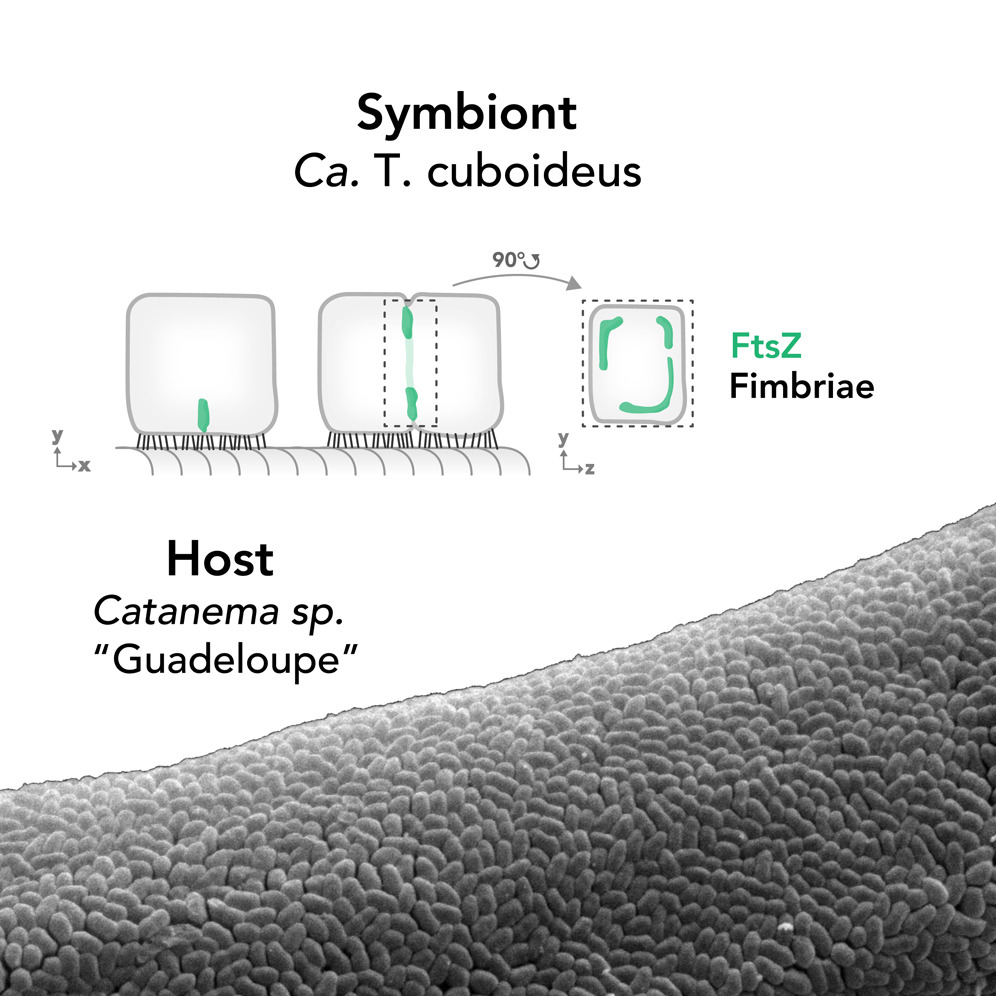
Cette bactérie se retrouve dans un milieu de vie un poil particulier car elle est symbiotique d’un ver nématode marin guadeloupéen du genre Catanema, et pullule sur sa cuticule (l’équivalent de sa peau). Pour s’y attacher, elle utilise des structures d’adhérences appelées fimbriae, et les chercheurs l’ayant découverte pensent qu’il pourrait s’agir là d’une explication de la forme particulière qu’elle adopte : maximiser la surface d’adhésion tout en limitant la possibilité d’être décrochées lorsqu’elles s’agencent les unes aux autres pour former une mono-couche bactérienne. Mais pour défendre son pré carré, pas question de proliférer dans n’importe quelle direction. À chaque division cellulaire, ces bactéries s’allongent le long de la cuticule du ver, formant temporairement un chapelet de deux perles carrées, puis se scindent pour donner deux bactéries filles adoptant la forme cubique d’origine.

Le comble donc, c’est que malgré leur forme idéale pour le rangement, en se divisant, ces bactéries cubiques s'organisent comme la pire chaussée pavée.

On ne peut donc pas compter sur la nature pour être carrée en affaires… Qu’à cela ne tienne, il existe des laboratoires qui sont spécialistes de la coupe au carré et qui cherchent à faire pousser des organismes selon cette forme. Pour cette chronique, je n’avais pas à chercher très loin parce que dans mon propre institut, l'Institut Jacques Monod, le directeur adjoint et de recherche Nicolas Minc a passé une petite partie de sa carrière à mettre des cellules en boîte. En 2011 notamment, il co-signait un article paru dans la revue Cell décrivant ce qui arrive à des cellules-œufs d’oursins lorsqu’on les place dans des sortes de moules microscopiques de tailles et formes variées : rond, cône, étoile, triangle, rectangle et bien sûr carré !

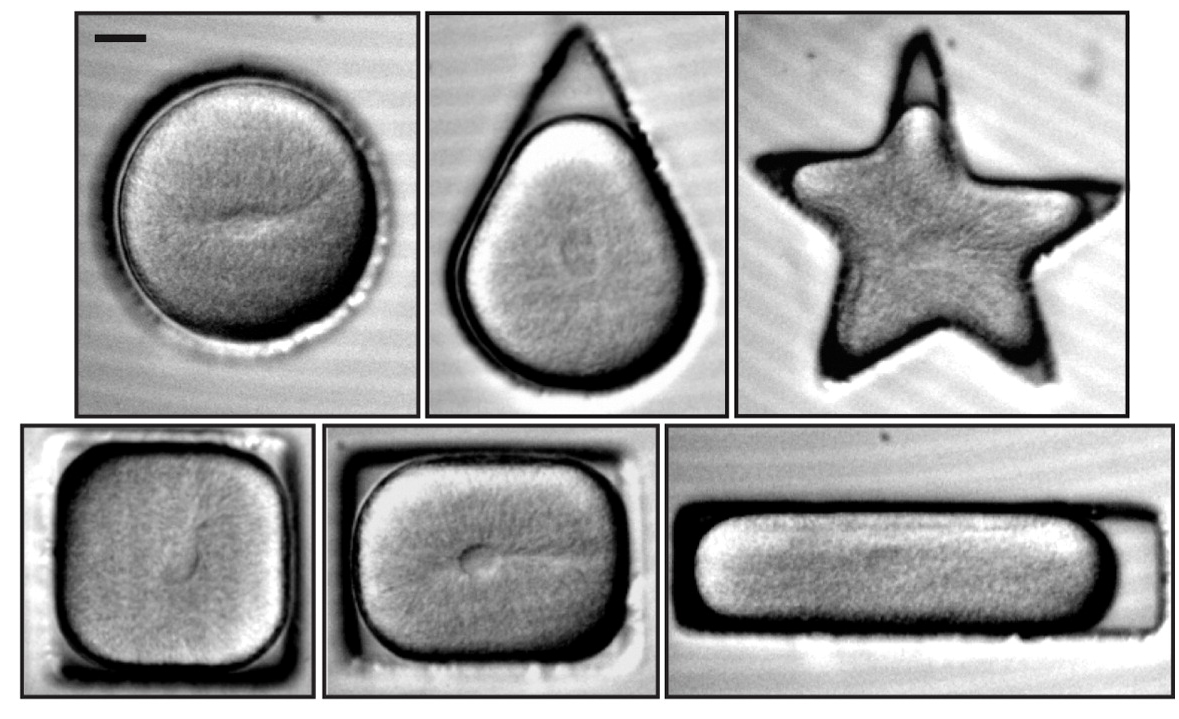
Ces moules sont réalisés en PDMS (Polydiméthylsiloxane) qui est à la base des caoutchoucs silicones et propice à la microfabrication de structures aux formes et dimensions hyper précises. Et ici, vu que les oeufs d’oursins fraîchement fécondés ont une forme parfaitement sphérique aux dimensions connues, on peut préparer des moules légèrement moins grand pour que, lorsqu’on dépose une lamelle de verre, celle-ci pousse et aplatit les oeufs dans chaque moule, les y confine et les oblige à adopter la forme géométrique d’intérêt.

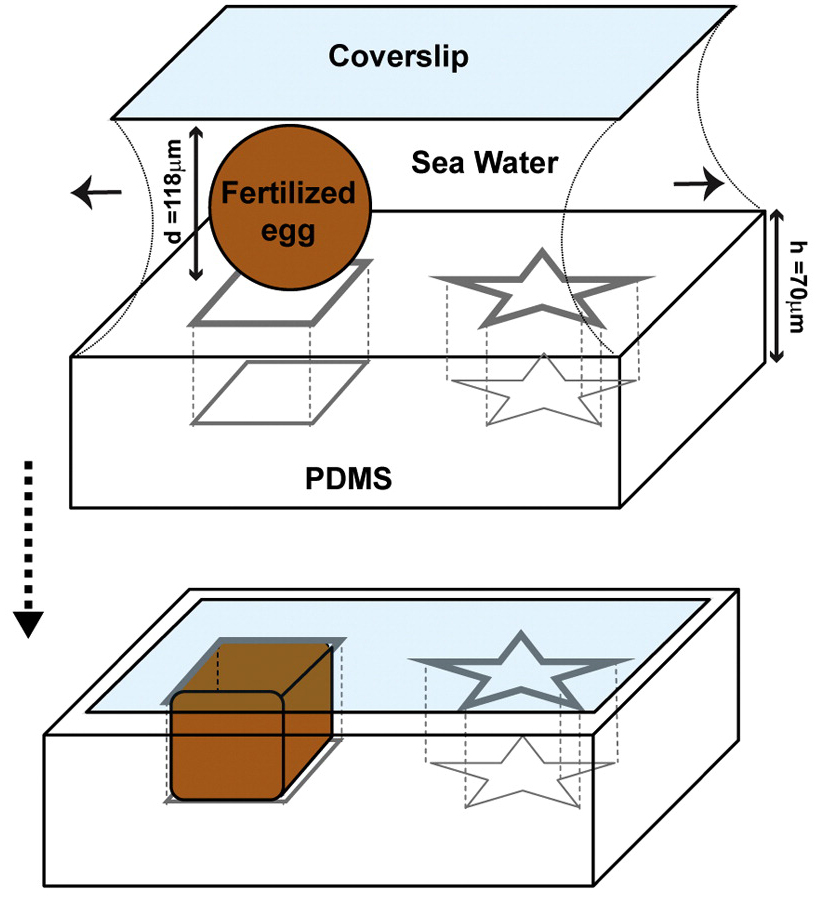
Mais d’ailleurs pourquoi diable contraindre ainsi la forme de ces cellules ? Et bien ce qui intéresse Nicolas Minc, c’est de comprendre comment une cellule va se diviser lorsqu’on change ainsi sa forme. L’idée était notamment de tester une règle empirique, la règle de l’axe long ou règle de Hertwig, censée prédire l’axe de division d’une cellule en fonction de sa forme. Pour déterminer cet axe, il faut localiser le centre de masse de la cellule et identifier l’axe le plus long qui traverse ce point : la division devrait se faire alors perpendiculairement à ce grand axe.

En proposant donc de visualiser le résultat des divisions de cellules d’oursins aux formes diverses et variées, c’est un peu comme si Nicolas Minc défiait le bluff d’Hertwig en ne croyant pas à la possibilité d’un carré d’as… Et il a eu raison de douter, car si dans certains moules, la règle d’Hertwig se vérifie, ce n’est pas le cas dans toutes les configurations, notamment lorsqu’une cellule prend la forme d’un carré :

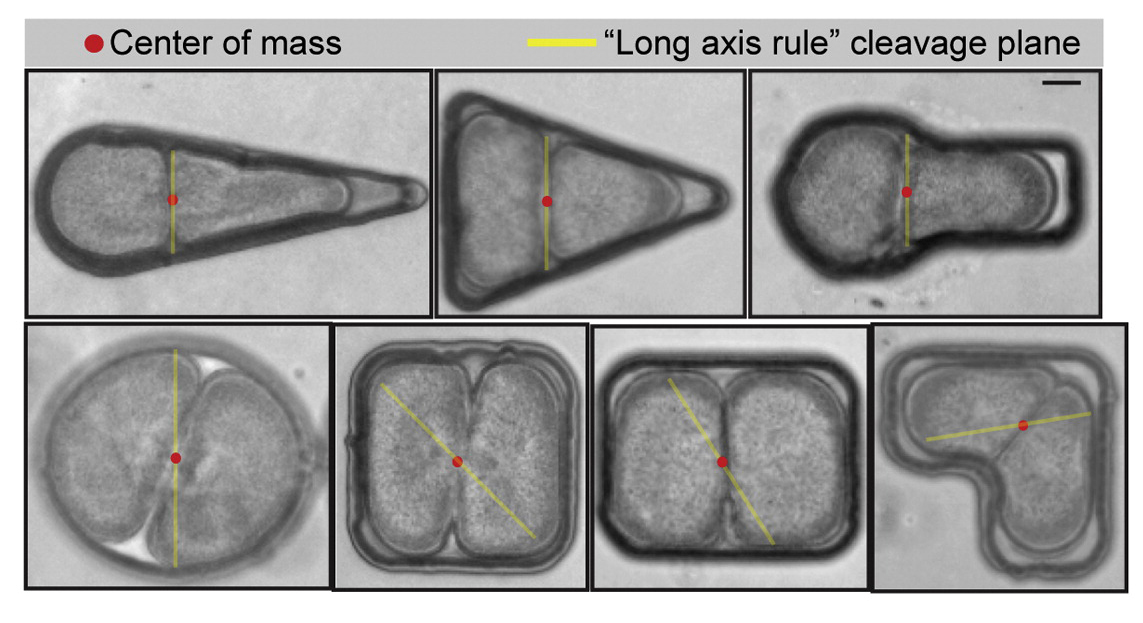
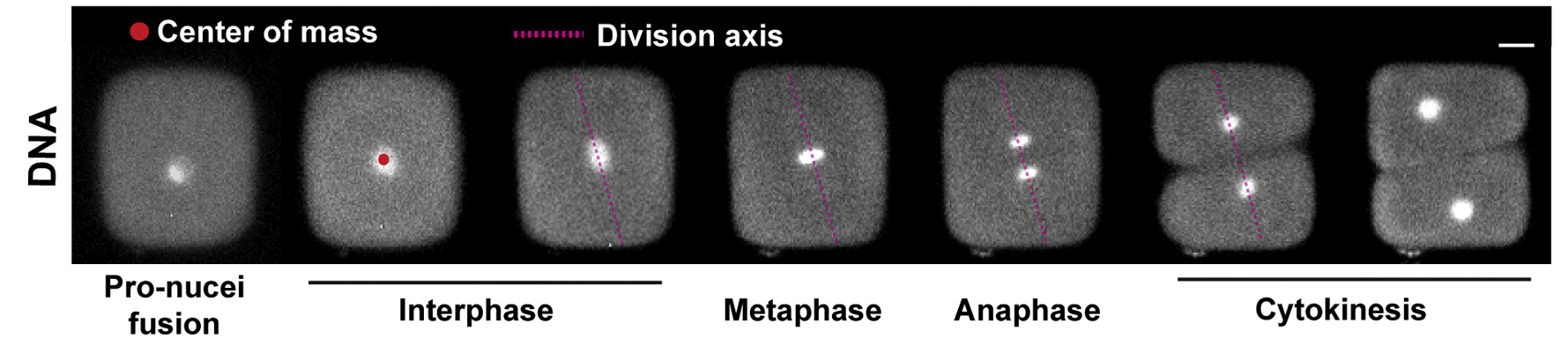
Si la règle d’Hertwig s’appliquait, on devrait obtenir une division selon une diagonale qui est l’axe le plus long traversant le centre de masse de la cellule. Or c’est plutôt le long de l’axe de symétrie de la cellule que se divise l'œuf carré… En suivant de près chaque étape de la division cellulaire, Nicolas Minc et ses collègues ont pu déterminer que la position et la forme du noyau dans la cellule était un meilleur prédicteur de l’axe de division… En effet, en configuration carrée, le noyau de la cellule se déplace bien au centre mais se déforme aussi un peu, prenant un aspect oblong qui définit un axe. Et c’est selon un plan perpendiculaire à cet axe que la division va s’effectuer.

Fort de cette observation, les chercheurs ont développé un modèle complexe de prédiction du plan de division, prenant en compte des composants du squelette cellulaire qu’on appelle des microtubules, et plus précisément leur longueur et la force qu’ils peuvent exercer sur le noyau. Je crains par contre que vous expliquer en détail ce modèle computationnel vous mettrait rapidement la tête au carré…

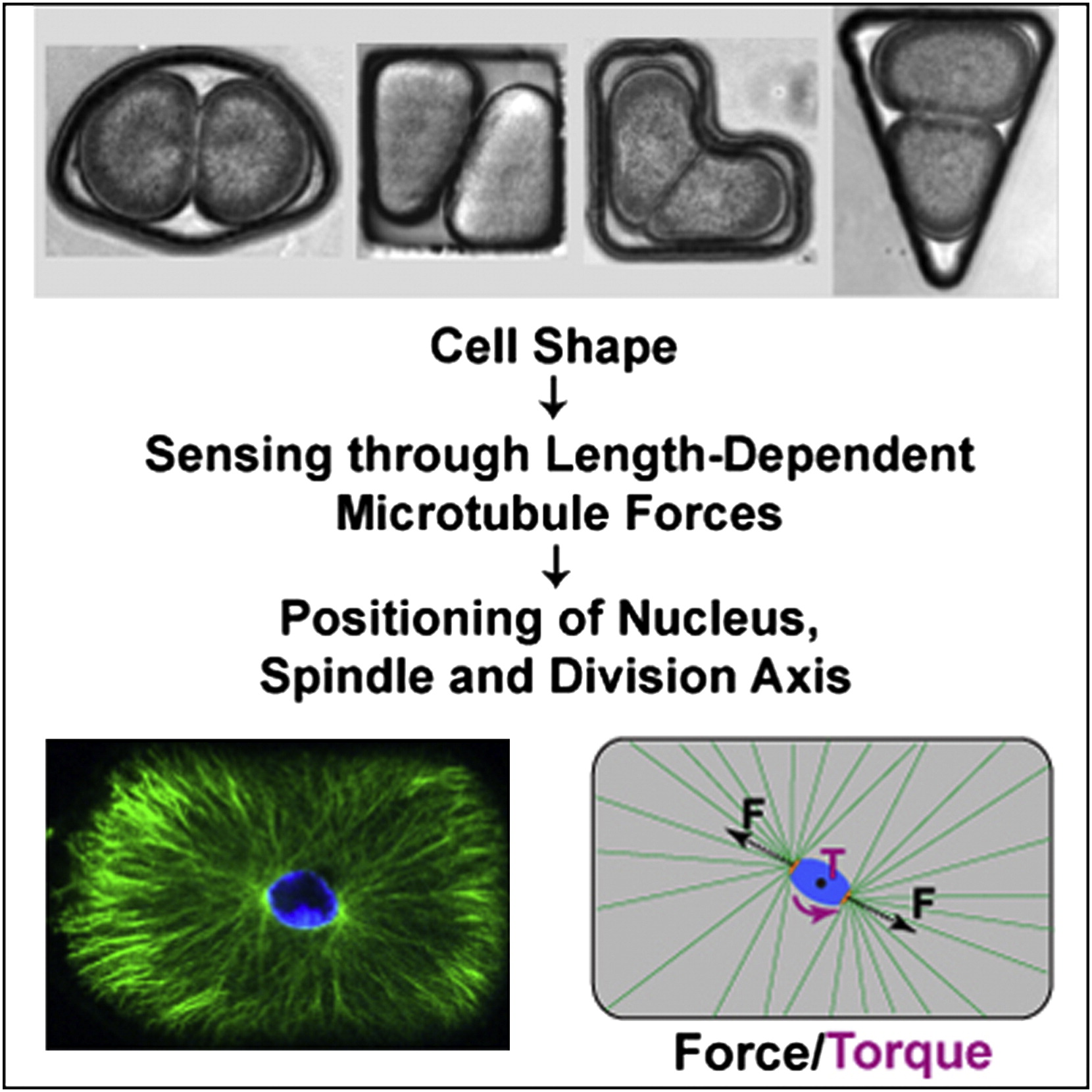
Désolé, ce n’est pas très carré de terminer ainsi ma chronique… j’aurais dû passer plus de temps à la peaufiner plutôt que de me promener dans le square…

Liens :
The Echinoblog: Saturday special Fresh from Japan: A square-shaped Bat Star! & RAZOR STARFISH!!
Square microbe grown in laboratory - ABC Science
Haloarcula quadrata - Wikipedia
A Game of Dice
Article HighMag

Références :
Minc, N., Burgess, D., & Chang, F. (2011). Influence of cell geometry on division-plane positioning. 144(3), 414‑426. https://doi.org/10.1016/j.cell.2011.01.016
Walsby, A. E. (1980). A square bacterium. Nature, 283(5742), 69‑71. https://doi.org/10.1038/283069a0
Weber, P. M., Paredes, G. F., Viehboeck, T., Pende, N., Volland, J.-M., Gros, O., VanNieuwenhze, M., Ott, J., & Bulgheresi, S. (2022). FtsZ-mediated fission of a cuboid bacterial symbiont. iScience, 25(1), 103552. https://doi.org/10.1016/j.isci.2021.103552