Cherche règle de Golomb

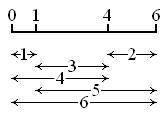
Une règle de Golomb est une règle munie de marques à des positions entières, telle que deux paires de marques ne soient jamais à la même distance; en d'autres termes, chaque couple de marques mesure une longueur différente des autres.
L'ordre d'une règle de Golomb est le nombre de marques qu'elle porte; la longueur d'une règle de Golomb est la plus grande distance entre deux de ses marques. La plus courte règle de Golomb pour un ordre donné s'appelle une règle de Golomb optimale.
Construire une règle de Golomb n'est pas difficile mais trouver toutes les règles de Golomb d'un ordre donné est un défi informatique et un projet de calcul distribué (voir distributed.net) est actuellement en cours pour trouver des règles de Golomb optimales.
Le portail de L'Alliance Francophone des projets BOINC nous annonce que le projet OGR-25 est terminé.
"Il y maintenant plus de huit ans, les participants au projet distributed.net (dnetc) débutaient une recherche complète de toutes les règles de Golomb d'ordre 25 pour découvrir la ou les règles optimales. L'année 2008 restera comme l'année de l'aboutissement de cet effort. Les utilisateurs viennent de démontrer par une recherche exhaustive que la règle découverte par M. D. Atkinson et A. Hassenklover en 1984 est réellement la règle de Golomb d'ordre 25 optimale."
OGR-25 est terminé. Place à OGR-26 !
C'est le mathématicien Solomon W. Golomb qui est à l'origine de l'idée de règle de Golomb.
On lui doit aussi la suite de Golomb; il s'agit de la suite croissante d'entiers naturels définie de la façon suivante : pour tout entier n supérieur ou égal à 1, le n-ième terme de la suite de Golomb est le nombre d'occurrences de l'entier n dans cette suite.
Sauriez-vous trouver les premiers termes de cette suite, avant de consulter Wikipédia ?