Pavages

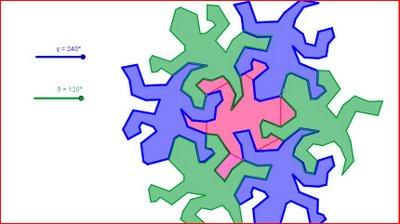
Un pavage (ou dallage) est une partition d'un espace (généralement un espace euclidien comme le plan ou l'espace tridimensionnel) par un ensemble fini d'éléments appelé tuiles
Pour paver le plan avec des lézards,cliquer sur l'image
Généralement, on considère des pavages par translations, c'est-à-dire que deux mêmes tuiles du pavage sont toujours déductibles l'une de l'autre par une translation.
Les mathématiciens ont longtemps pensé que les seuls pavages par translations du plan étaient nécessairement périodiques (répétitifs).Notamment, Hao Wang a conjecturé en 1961 que c'était le cas, et en a déduit qu'on pouvait concevoir un programme informatique qui déciderait si un jeu de tuiles donné permettait de paver ou non le plan. Cependant, en 1964, Robert Berger (un élève de Wang) a trouvé un ensemble de 20 426 tuiles ne pouvant paver qu'apériodiquement le plan. La conjecture est donc fausse : savoir si un jeu de tuiles peut paver ou non le plan serait indécidable Il existe aussi des pavages d'espaces non euclidien (espaces hyperboliques) les plus célèbres étant sans doute les nombreux pavages de M.C. Escher * comme celui-ci:

*Maurits Cornelis ESCHER est né le 17 juin 1898 à Leeuwarden, en Frise (PAYS-BAS). Son père est ingénieur hydraulicien. Alors que ses frères ont des cursus scolaires scientifiques, il semble que les seuls points lumineux de ses études secondaires soient les cours de dessin. Ce qui est sûr, c'est qu'il ne manifeste aucun don pour les mathématiques et la physique ! Les mosaïques des Maures décorant le palais de l'Alhambra à Grenade et la mosquée de Cordoue, ces vestiges de l'Espagne islamique du Moyen-Âge, ont grandement impressionné Escher dès sa première visite en 1922. En 1936, durant un second séjour, il passe plusieurs jours à copier ces ornements, aidé par son épouse Jetta. La possibilité de remplacer les formes géométriques des motifs par des éléments reconnaissables deviendra pour lui une véritable passion.

P.S. Si la géométrie hyperbolique vous attire,allez faire un tour ici