Trois images pour un résultat – ou plus si affinités!

Une de mes caractéristiques est que je suis toujours à la recherche de méthodes pour que la représentation des données soit percutante. Même si ça implique de passer par des transformations bizarres, des rapports, et des heures à écrire du code en R pour faire des choses étranges – et write-only. Et par conséquent, j’aime vraiment quel les figures livrent instantanément leur message. Même si des fois, ça implique d’utiliser trois figures, pour être sûr.

Dans un papier récemment accepté et pas encore paru [Poisot T. & Desdevises Y. (2010) Putative speciation events in Lamellodiscus (Monogenea‚ Diplectanidae) assessed by a morphometric approach, Biological Journal of the Linnean Society], nous avons trouvé qu’une espèce de parasites se divisait en deux populations sur une même espèce d’hôtes, mais que ces deux populations étaient sur des groupes d’individus différents.

La première étape était de montrer que les deux populations se différenciaient par leur morphométrie :

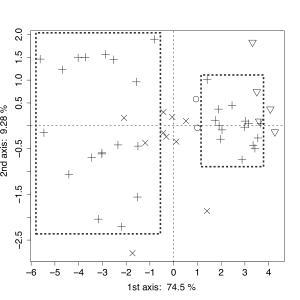
On voit bien que les individus symbolisés par un + (chaque espèce d’hôte possède un symbole) forment deux groupes, vraiment différents sur des considérations purement morphométriques. Il faut ensuite quantifier cette différence : est-ce qu’elle est signficative? Le premier graphique est le résultat d’une analyse en composantes principales, qui est une analyse exploratoire et pas un test statistique. Et il nous fallait confirmer la séparation en ayant une valeur de support, une certaine confiance dans notre résultat.

Comme le premier axe (les bases de l’ACP sont un peu complexes, disons que le premier axe correspond à la projection des données sur un vecteur qui explique le mieux leur distribution) explique presque 75 % de la variance (c’est beaucoup, comparez avec les 42 % que j’avais présenté précédemment), nous avons utilisé ce premier axe comme une valeur qui « résume » la morphométrie (la « forme » des organes).

Il a donc fallu montrer que ces deux groupes existaient, sans faire l’hypothèse de les séparer a priori. Nous avons donc plutôt choisi de montrer que la distribution des données n’était pas unimodale : autrement dit, si on ne peut pas dire que ces deux choses sont différentes, on va montrer qu’elles ne sont pas identiques, en utilisant le Hartigan & Hartigan Dip-test of unimodality.

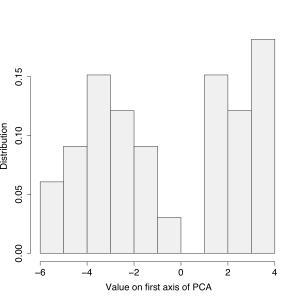
Comme vous le voyez sur cette figure, on a deux distributions des valeurs sur le premier axe, autrement dit, deux populations distinctes! Il ne reste plus qu’à vérifier que ces deux populations sont réparties sur des hôtes différents.

Pour ça, nous avons pris l’ensemble des mesures morphométriques, et nous avons construit une matrice de distances, utilisée pour construire un arbre UPGMA, sur lequel nous avons appliqué une procédure de bootstrap non-paramétrique. Tout ce jargon pour dire qu’en fait, on a mesuré la probabilité d’avoir de la structure dans nos données. Plus les valeurs des branches sont proches de 100, plus on a de chances que le branchement observé soit réel (et donc, que la séparation aie un sens).

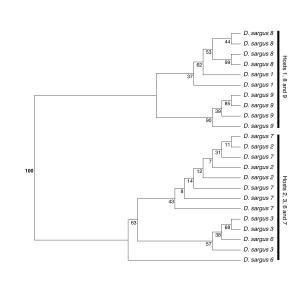
Et nous observons que le nœud le plus à la base de l’arbre, celui à partir duquel les deux populations ne se mélangent plus, est soutenu dans 100 % des cas. Autrement dit, nous avons montré que (i) deux populations de ce parasite semblent coexister, que (ii) la différence entre les deux est significative, et qu’enfin (iii) ces deux populations ne sont pas partagées entre des individus hôtes. Ce qui est plutôt cool et inattendu comme résultat.

Si quelqu’un à d’autres suggestions à faire pour la représentation de ces données, je suis preneur!

Billets similaires