Ce n'est pas l'explorateur Jacques Cartier, ni même le mathématicien Pierre (né en 1932) l'auteur de cette formule. C'est celle de la Fondation Cartier (nommée d'après le joaillier Louis Cartier 1875-1942) et de son exposition de mathématiques, déjà évoquée dans ce blog. Je vous donne cette formule :
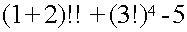
Oui, vous avez déjà trouvé de tête, bravo !, , çà donne 6 ! + 36² - 5 = 720 + 1296 - 5 = 2011. C'était une des "attractions" de l'exposition : trouver 2011 en utilisant des opérateurs mathématiques sur des chiffres qui se suivent, à partir de 1 (la formule fait intervenir dans l'ordre 1, 2, 3, etc.), et ce bien évidemment en le moins de chiffres possible.
Ceci se faisait non sur un tableau noir avec une craie (les maths à l'ancienne) mais sur un tableau électronique : celui-ci vous disait quand vous trichiez (mettre deux chiffres non successifs) - il enregistrait aussi les "meilleures formules" (comme au flipper les meilleurs scores).
Je défie quiconque, debout, sans calculette, avec des gens regardant derrière, de trouver in situ dans des délais raisonnables cette magnifique formule. D'ailleurs les "meilleures formules" enregistrées étaient toujours des variations autour de celle-ci, avec des parenthèses et des crochets en plus... ce que ne détectait pas cette idiote de machine. J'avais moi-même péniblement trouvé, avec mon fils, une formule montant jusqu'à 12, que je ne me rappelle plus et qui n'a pas d'intérêt, vu celle-là !
Mais une fois qu'on voit la formule, on peut la commenter. Ce que nous allons faire.
D'abord (là c'est le mauvais joueur qui parle), le jeu ne disait pas qu'on pouvait utiliser les "doubles factorielles". Les indications mentionnaient toutefois l'opérateur factorielle.Du coup, je pense qu'on peut utiliser les doubles exponetiations (ce qui peut être utile pour les très grands nombres).
Ensuite, je me demandai pourquoi ce n'était pas 2012 qu'il fallait trouver (ceci dit l'exposition avait commencé en 2011). Eh bien parce que c'est nettement moins élégant (au sens... mathématique) pour 2012. Sauf si un lecteur du blog trouve une formule meilleure, la sule que je vois est de poursuivre la formule ci-dessus en retranchant 6 et en ajoûtant 7... Ce qui montre au passage qu'on peut virtuellement construire tout nombre ainsi, avec cette formule (assez élégante dans sa graphie, mais pas dans sa longueur - écrivez-la pour 2011 ou 2012 si vous y tenez) :
1 - 2 + 3 - 4 + 5 - ...
Mais c'est le premier terme de la formule ci-avant qui attire l'attention, (1+2)!!. Je pense que c'est le plus grand nombre (720) qu'on peut atteindre avec 1 & 2. Car le seul moyen d'utiliser rentablement 1, c'est par l'addition : en multiplication, puissance, factorielle, il ne "vaut" rien.
Si l'on y met 3, on obtient (1+2+3)!! soit 720 ! (factorielle de 720), nombre qui dépasse déjà l'entendement ; ou si l'on écrit sans la double factorielle (1+2+3)!, on obtient le même résultat que pour (1+2)!! mais en ayant "gâché" le chiffre 3. Le (1+2)!3 est toutefois à retenir, donnant 216, et nous mettant au départ dans des gammes de nombres plus petits - mais qu'on peut rattraper par la suite avec des 45, etc. Ce n'est pas parce qu'on démarre par un plus petit nombre qu'on ne peut pas passer la vitesse supérieure après...
Bref, ce jeu est assez amusant, même a posteriori.
PS : Le jeu que je vous propose, en commentaires, est plus simple : vous contruisez vous-même une formule de Cartier que vous jugez "esthétique" (en utilisant des nombres successifs - NB: pour la graphie d'exponentiation, on peut utiliser ^), et vous la faites deviner en commentaires ! Attention pas sérieux s'abstenir : vous nous faites réfléchir sur un vrai résultat (pas du bidon) - pour preuve vous donnez la réponse deux jours après...

