Probabilité de la main crève-coeur avec moins que 10 joueurs à la table

Dans un billet précédent, il a été question de la probabilité de la main crève-coeur pour une table de 10 joueurs ne couchant jamais leurs cartes. Il s'agit ici de Texas Holdem.

Sur EspaceJeux, certaines tables sont cependant limitées à 6 joueurs maximum. De plus, il doit y avoir au minimum 4 joueurs pour que la main crève-coeur soit valide.
Dans ce billet, je vous invite à examiner comment varie la probabilité d’une main crève-coeur (carré de valets ou mieux) à des tables entre 4 et 10 joueurs.
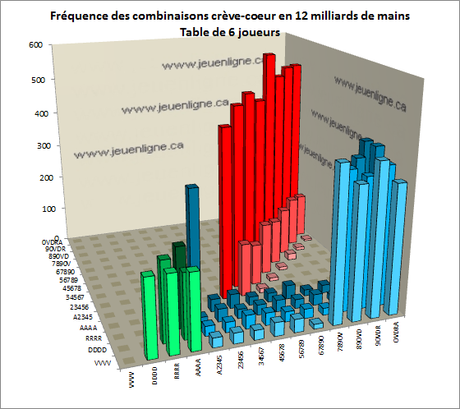
Commençons par simuler des tables de 6 joueurs ne couchant jamais leurs cartes. En utilisant le même simulateur, il a fallu simuler 12 milliards de mains, au lieu de 4 milliards, pour obtenir une précision similaire. À 10 joueurs, un carré de valets ou mieux avait une chance sur 336.700 d’être battu (voir billet précédent). À 6 joueurs, cette probabilité a diminué à une chance sur 1.060.539, c’est-à-dire 3,15 fois moins.

Voici la fréquence des mains crève-coeur obtenues lors des 12 milliards de mains simulées. À très peu de différence, c’est une configuration similaire à celle obtenue avec les tables de 10 joueurs … sauf qu’il a fallu trois fois plus de mains pour y parvenir. Ainsi, passer de 10 à 6 joueurs fait diminuer également, par environ trois, toutes les fréquences des combinaisons possibles. Il n’y a pas de combinaison plus particulièrement affectée.

Cette division uniforme est facile à expliquer et généralisable à n’importe quelle table incomplète. Calculons d’abord le nombre de mains qui se confrontent à une table de 10 joueurs. Le joueur 1 est opposé à neuf joueurs. Si on ne compte pas une confrontation deux fois, le joueur 2 est confronté à huit joueurs. Le joueur 3 à sept joueurs, et ainsi de suite. À chaque brassée, si personne ne couche ses cartes, il y a donc 45 confrontations deux à deux (9+8+7+6+5+4+3+2+1). À une table de 6 joueurs, seulement 15 confrontations sont possibles (5+4+3+2+1). C’est trois fois moins.

Pour généraliser à n’importe quelle table, l’équation est simple. Le nombre de confrontations est égal au nombre de joueurs au carré moins le nombre de joueurs, et tout ça divisé par deux ((N x N) – N) / 2. Avec un minimum de 4 joueurs à la table, il y a 6 confrontations possibles. Par rapport à une table pleine de 10 joueurs, la probabilité est divisée par 7,5 (c’est-à-dire 45/6).

Dans la figure ci-contre, les estimés sont fondés sur la mise en commun des deux simulations. Conséquemment, ces estimés sont un peu différents des estimés publiés précédemment, mais ils sont statistiquement plus exacts. Le paramètre additionnel qu’on veut obtenir est la probabilité d’une main crève-coeur (carré de valets ou mieux) pour une seule confrontation. À une table de 10 joueurs, la probabilité d’une chance sur 344.902 divisée par 45 confrontations est égale à ,00000006443 (une chance sur 15.520.586). À une table de 6 joueurs, on obtient le même nombre si on divise la probabilité d’une chance en 1.034.706 par 15. Bref, pour n’importe quelle table, la probabilité de la main crève-coeur (carré de valets ou mieux) est égale à ,00000006443 fois ((N x N) – N) / 2 … où N est le nombre de joueurs à la table.
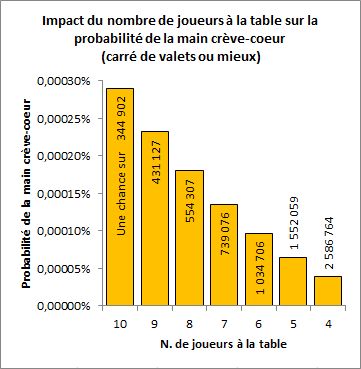
Dans ce raisonnement, nous avons pris pour acquis que, à six joueurs, la probabilité était exactement trois fois moindre qu’à 10 joueurs. Mais, en comparant les simulations, la probabilité était plutôt 3,15 fois moindre. Une première explication de l’imprécision se trouve certainement dans le fait qu’il faudrait encore plusieurs milliards de mains pour calculer adéquatement la probabilité des confrontations de quintes n’ayant qu’une carte commune (voir billet précédent). Dans chacune des simulations, chacune de ces quintes n’a été observée que 10 fois en moyenne. Statistiquement, c’est encore insuffisant.

Une seconde explication de l’imprécision découle du fait que le hasard n’est pas réel mais simulé par un générateur de nombres pseudos aléatoires (GNPA). Les GNPA sont des processus chaotiques, plutôt qu’aléatoires, qui induisent nécessairement une distorsion des probabilités.

Enfin, une troisième explication pourrait être qu’il n’y a pas vraiment d’imprécision. Il y a peut-être un autre aspect de la situation qui devrait être pris en considération. Par exemple, s’il y avait 23 joueurs à la table, 46 cartes cachées seraient distribuées aux joueurs et cinq cartes seraient exposées sur la table. Il n’en reste donc plus qu’une seule dans le sabot. Est-ce que le nombre de cartes inutilisées influence aussi la probabilité? Ça y est. Le simulateur est reparti. La suite … un peu plus tard … dans quelques milliards de mains. Ce ne sera pas long.
Photo décolorée : Nevit