Nous avons vu avec Berger, dans notre précédent billet, pourquoi il n’y a que 5 polyèdres réguliers (convexes) – nous nous sommes pour cela appuyés sur la relation d’Euler S – A + F = 2 (nombre de sommets S, d’arêtes A, de faces F), valable pour tout polyèdre convexe. Toujours avec Berger, voyons une extraordinaire démonstration de cette relation, démonstration qu’il appelle affine.
On prend n’importe quel polyèdre convexe, et on imagine le couper par un plan qu’on va progressivement faire descendre du sommet supérieur du polyèdre (en le mettant dans une position donnée, peu importe) au sommet inférieur. Le dessin ci-dessous parlera mieux que moi (j’adore ces dessins manuscrits de Berger, nous en avions déjà utilisé un là).
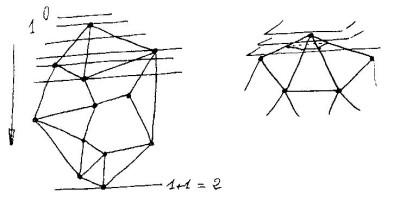
On peut prendre n’importe quelle direction de plan, à une condition : que ces plans parallèles ne contiennent jamais plus d’un sommet du polyèdre (on se convaincra aisément que c’est une condition facilement réalisable). On va alors faire le compte en faisant descendre le plan. En haut, quand le plan touche le sommet sans être entré dans le polyèdre, la somme (on appelle ainsi S – A + F, par simplification) vaut 1 (S=1, A=F=0). En entrant depuis le sommet du haut dans le polyèdre, on capte autant de faces que d’arêtes (du sommet partent h arêtes, et le sommet appartient à h faces – comme déjà écrit, pour s’en convaincre, aplatir le voisinage du sommet sur un plan, et constater qu’il y a dans ce voisinage autant d’arêtes que de faces, i.e. autant d’arbres que d’intervalles) : donc S reste égal à 1. Continuons à faire descendre notre plan de coupe, et l’on rencontre un premier sommet dans cette descente (à chaque fois, l’on n’en rencontre qu’un puisque c’est la condition imposée au plan de coupe). Notre somme s’incrémente de +1 (le sommet), mais regardons ce qui se passe au niveau F et A. Je fais un dessin aplatissant le sommet, moins joli que celui de Berger.
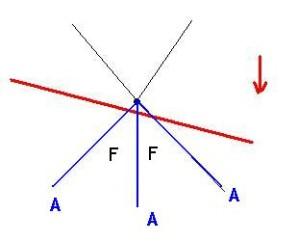
À chaque traversée de sommet, S gagne 1, (A-F) gagne 1, S-A+F reste
stable.
Le plan et son sens de descente sont en rouge. Il va « capter », dans ce cas, h’ nouvelles arêtes (ici 3), et h’ – 1 nouvelle faces (ici 2). Sur un sommet traversé, le nombre d’arbres (arêtes) n’est pas égal au nombre d’intervalles (faces), car les nouvelles arêtes « encadrent » les nouvelles faces. Ce qui fait qu’au passage d’un sommet qui n’est ni le premier ni le dernier, on a :
Avant
Après
sommets
S
S + 1
arêtes
A
A + h’
faces
F
F + h’ - 1
Somme d’Euler
transitoire
S – A + F = 1
(comme au départ)
(S +1) – (A+ h’) + (F + h’ – 1)= S – A + F
(inchangée)
Là, j'ai un peu trop décortiqué pour convaincre (ce qui m'oblige à introduire une variable h'). Une manière plus concise : pendant la “traversée” du polyèdre par le plan de coupe, la somme reste égale à 1, puisqu’à chaque sommet S s’incrémente de 1, mais (A-F) aussi, ce qui fait que S – A + F reste constant, égal à sa valeur de départ, 1. Jusqu’à récupérer le dernier sommet, en bas, où il n’y a plus faces et arêtes en dessous, et la somme s’incrémente de 1 (le dernier sommet), pour arriver à 2. Comme l’écrit Berger sur son dessin, et c'est bien connu, 1 + 1 = 2. CQFD.
1. Pour aprofondir, on s'aperçoit avec Wikipédia que Descartes avait déjà trouvé dans un manuscrit inédit (écrit en 1680) la relation qu'Euler formalise en 1752, ce qui fait qu'en France (surtout sur Wikipédia, car pour ma part j'ai toujours entendu 'Relation d'Euler'), on appelle cela Théorème de Descartes-Euler.
2. Plus intéressant, on trouvera aussi une extraordinaire généralisation aux dimensions supérieures par Poincaré 1893, Wikipédia : sans se soucier des termes topologiques peu simples, retenons que S – A + F vaut alternativement 0 (dans toutes les dimensions paires, à commencer par 2, dans le plan avec des polygones) ou 2 (dans toutes les dimensions impaires, à commencer par 3, dans notre espace avec des polyèdres).

