Ce matin en faisant une requête sur google, pour trouver l'adresse du service d'ORL de l’hôpital Lariboisière à Paris, j'ai fait une erreur j'ai tapé HPP au lieu de APHP et voici le contenu proposé par Wikipédia...! Je ne sais pas si cela répond à mes problème d'équilibre...?
Alors, pour tout x dans I, l'expression
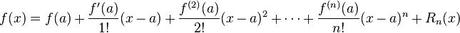ou son équivalent
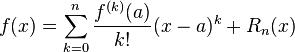définit un reste Rn(x) dont le
comportement s'apparente au monôme (x – a)n + 1.
En mécanique
des milieux continus, HPP désigne l'Hypothèse des Petites
Perturbations (sous-entendu d'un état d'équilibre). Elle permet d'envisager une
linéarisation
des équations statiques ou dynamiques décrivant l'état, ce qui simplifie à
la fois l'analyse théorique et le traitement numérique. Dans ce procédé, seul le
premier ordre du développement
de Taylor (autour des valeurs d'équilibre) est conservé, ce qui est légitimé
par l'HPP.
Cette hypothèse est à la base du calcul des fréquences et
mouvements propres.
Paris - 17:00 - Temps clair - 27°C
Précipitations : 0% - Humidité : 45% - Vent : 2 km/h
Jeu de briques
Snake
Pacman
Bubble