Exercice théorème de thévenin et Théorème de Superposition exo+corrigés

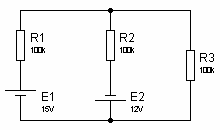
Théorème de Superposition et théorème de théveninExercice 1Utiliser le théorème de superposition pour calculer le courant qui circule dans R3
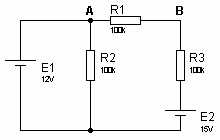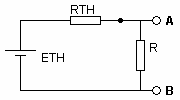
Exercice 2Utiliser le théorème de superposition pour calculer la tension U_AB aux bornes de R1.Exercice 3Utiliser le théorème de superposition pour calculer la tension aux bornes de R1.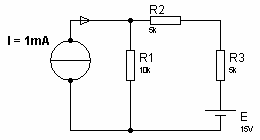Exercice 41. Dessinez le générateur de Thévenin de la figure suivante, sans tenir compte de la résistance R.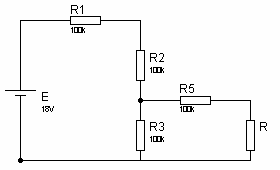

2. pour R = 150 kΩ      a. Déterminez le courant qui traverse R      b. calculer la puissance fournie à RExercice 5Déterminer les caractéristiques ET et RT du générateur de Thévenin équivalent au circuit suivant, sans tenir compte de la résistance R.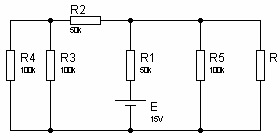Exercice 6Dans le montage suivant, déterminer le courant I circulant dans la résistance R = 100k.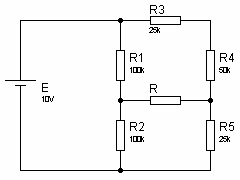Exercice 71. Dessinez le générateur de Thévenin de la figure suivante, sans tenir compte de la résistance R.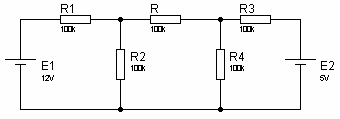2. Calculez la tension UR et la puissance fournie à la résistance R.Exercice 8Dessinez le générateur de Thévenin de la figure suivante, sans tenir compte de la résistance R.------------------------------------------------------------------------------------------------

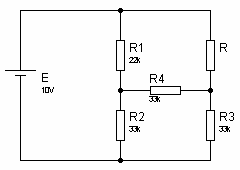CORRECTION - SOLUTIONS

------------------------------------------------------------------------------------------------

Solution Exercice 1

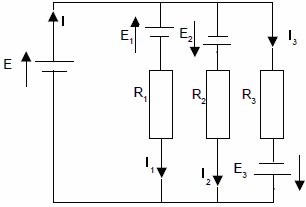
Pour calculer le courant qui circule dans R3, on calcule la tension aux bornes de R3.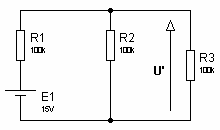fig1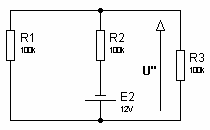fig21- on calcule la tension U’ (aux bornes de R3) avec E2 en court-circuit (fig1)U’ = E1 x (R2 // R3) / [(R2 // R3) + R1] = 15V x 50 / 150 = 5V2- on calcule la tension U’’ (aux bornes de R3) avec E1 en court-circuit (fig2)U’’ = -E2 x (R1 // R3) / [(R1 // R3) + R2] = -12V x 50 / 150 = -4V3- la tension U aux bornes de R3 est : U = U’ + U’’ = 1V4- I = U / R3 = 1V / 100k = 10μA

Solution Exercice 2

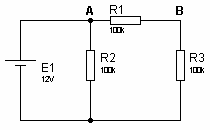fig3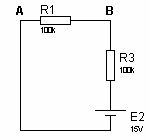fig4
1- on calcule la tension U’AB avec E2 en court-circuit (fig3)U’AB = E1 x R1 / [R3 + R1] = 12V x 100 / 200 = 6V2- on calcule la tension U’’AB avec E1 en court-circuit (fig4)U’’AB = - U’’BA = -E2 x R1 / [R1 + R3] = -15V x 100 / 200 = -7,5V3- UAB = U’AB + U’’AB = 6V – 7,5V = 1,5V

Solution Exercice 3

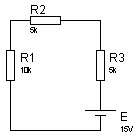fig5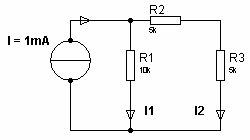fig6
1- on calcule la tension U’ avec le générateur de courant ouvert (fig5)U’ = E1 x R1 / [R1 + R2 + R3] = 15V x 10 / 20 = 7,5V2- on calcule la tension U’’ avec E en court-circuit (fig6)U’’ = I1 x R1 = I2 x (R2 + R3) = I x R1 // (R2 + R3) = 1mA x 10 x 10 / (10 +10) = 5V3- U = U’ + U’’ = 7,5V + 5V = 12,5V

Solution Exercice 4

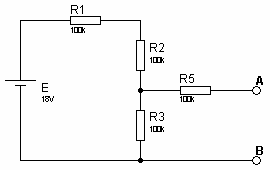fig7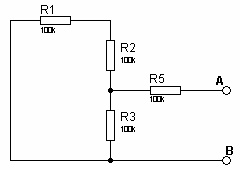fig8
1. Eth = UAB = E x R3 / ( R1 + R2 + R3) = 18 x 100 / (100 + 100 + 100) = 6VRth = RAB = R5 + R3 // (R2 + R1) = 100k + 100k x 200k / 300k = 166,67k2. pour R = 150 kΩa. I = Eth / (Rth + R) = 18,95μAb. P = R x I2 = 53,85μW

Solution Exercice 5

1. on calcule Eth = UAB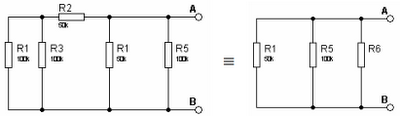R6 = R2 + R3 // R4 = 50k +100k //100k = 100kEth = UAB = E x (R5 // R6) / [R1 + (R5 // R6)] = 15V x 50k / 100k = 7,5V2. on calcule Rth = RAB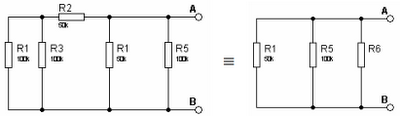Rth = RAB = R1 // R5 // R6 = 25k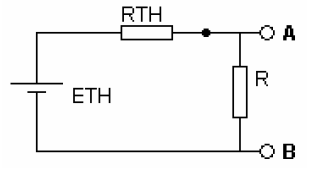

Solution Exercice 6

1. on calcule Eth = UAB et Rth = RAB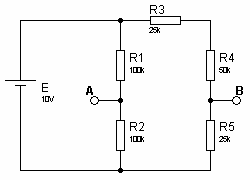Eth = UAB = UA - UBUA = E x R2 / (R1 +R2) = 10V x 100 / 200 = 5VUB = E x R5 / ( R3 + R4 + R5)UB = 10V x 25 / 100 = 2,5VEth = UAB = UA - UB = 5V – 2,5V = 2,5V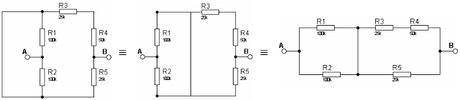Rth = RAB = (R1 // R2) + [R5 // (R3+R4)] = 100k // 100k + 25k // 75k = 50k + 18,75k = 68,75k2. pour R = 100 kI = Eth / (Rth + R) = 2,5V / (68,75k + 100k) = 14,81μA

Solution Exercice 7

1. on calcule Eth = UAB et Rth = RABEth = UAB = UA - UBUA = E1 x R2 / (R1 +R2) = 12V x 100 / 200 = 6VUB = E2 x R4 / (R3 + R4) = 5V x 100 / 200 = 2,5VEth = UAB = UA - UB = 6V – 2,5V = 3,5VRth = RAB = (R1 //R2) + (R3 // R4) = 100k // 100k +100k // 100k = 100k2. UR = Eth x R / (Rth + R) = 3,5V x 100k / (100k + 100k) = 1,75VPR = UR2 / R = (1,75V) 2 / 100k = 30,625μW

Solution Exercice 8

1. on calcule Eth = UAB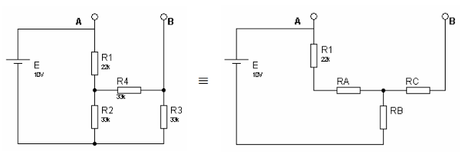On utilise la transformation triangle-étoile. Puisque R2 = R3 = R4 = 33k, RA = RB = RC = 33k / 3 = 11kEth = UAB = E x (R1 + RA) / (R1 + RA + RB) = 10V x (22k + 11k) / (22k + 11k +11k) = 7,5V2. on calcule Rth = RAB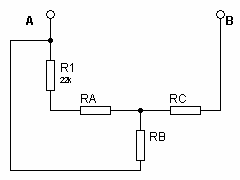Rth = RAB = [(R1 + RA) // RB] + RC = 33k // 11k + 11k = 19,25k3.