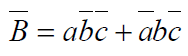Serie d'exercices sur le codage des nombres reels et l’algebre de boole

I- Codage des nombres réels

1. Convertir les nombres réels A= –124,75 et B=95,65 dans le format IEEE 754 simple précision puis en double précision.
Donner le résultat final sous forme de 8 digits hexadécimaux (en base 16)2. Déterminez la valeur décimale du nombre codé dans le format IEEE 754 simple précision N= 431F 562F(16). Donnez le résultat avec une puissance de 10.3. En admettant que le motif 0000 0000(16) et FFFF FFFF(16) sont des motifs valides en IEEE 754 simple précision, calculez les équivalents décimaux de ces nombres. Donnez le résultat avec une puissance de 10.4. Soit le nombre N= 431F 562F(16) codé dans le format IEEE 754 simple précision. Faites une extension de ce nombre dans le format IEEE 754 double précision.

II-Algèbre de Boole

L’ensemble E est muni d’une algèbre de Boole, on désigne par ā le complément de a, par a +b et ab la disjonction (ou) et la conjonction (et) de a et de b.1. Vérifier les égalités suivantes :

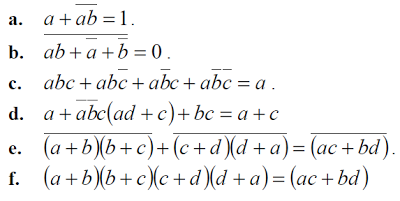
2. Donner les tables de vérité des 2 fonctions suivantes, puis les simplifier a l’aide d’un tableau de Karnaugh

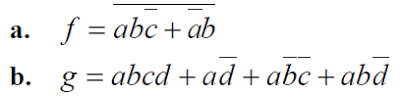
3. Soit la fonction booléenne A des trois variables a, b, c :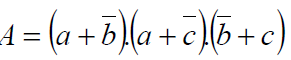a. Développer et transformer algébriquement A en une somme (ou) de produits (et).Montrer que :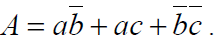
b. Simplifier A à l’aide d’un tableau de Karnaugh.
c. Simplifier A algébriquement.
d. Montrer que :

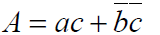
4. Soit la fonction booléenne B des trois variables a, b, c :

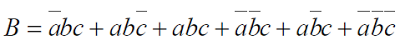
a. Simplifier B à l’aide d’un tableau de Karnaugh.
b. Montrer directement ce résultat par un calcul algébrique.
c. Montrer que :