Le hasard et les hypothèses en statistique

L'été est une période propice pour écrire sur des sujets moins habituels. C'est pourquoi, après mon billet sur la cryptomonnaie développée par Facebook, je vous propose de nous intéresser aujourd'hui aux règles qui permettent de décider si l'on doit rejeter ou non une hypothèse statistique sur la base des résultats obtenus sur un échantillon. En simplifiant à l'extrême, nous allons nous demander si les observations faites sur un échantillon d'une population relèvent du hasard de l’échantillonnage ou correspondent à un phénomène significatif... Pour montrer la méthodologie suivie par les statisticiens, tant en médecine que dans d'autres sciences expérimentales, nous allons nous appuyer sur un exemple concret.

Un cas concret

Chaque année, l'examen du baccalauréat suscite une hystérie inversement proportionnelle à la valeur réelle du diplôme. Ainsi, à peine les épreuves passées, voit-on fleurir des pétitions pour réclamer la clémence des correcteurs en raison d'un exercice jugé trop difficile, d'un auteur considéré comme peu connu, etc. D'ailleurs cette année, et c'est hélas historique, nous avons touché le fond, l'absence de certaines notes ayant conduit des jurys - sous injonction du ministère - à pratiquer des retouches plus que cosmétiques et surtout aberrantes : élèves passés au rattrapage en raison de l'attribution d'une note fictive (pardon, de contrôle continu dans les éléments de langage...) mais qui auraient dû être admis dès le premier tour, élèves qui vont apprendre dans quelques jours qu'ils ont finalement décroché une mention, élèves qui n’auraient jamais eu de mention si la note de contrôle continu n’avait pas été retenue, etc.

Mais revenons à nos moutons... Imaginons qu'au niveau national, le ministre de l'éducation nationale affirme au doigt levé qu'en Mathématiques la note moyenne en filière S est de 12/20. Il est bien entendu possible de calculer la moyenne de tous les élèves, mais le procédé est coûteux en temps et en argent, et l'on sait bien qu'un ministre se doit de parler plus vite que son ombre dans les médias. Dans cet exemple, on suppose donc que le ministre n'a pas connaissance à ce moment de la vraie moyenne (sinon, il n'y a plus lieu de faire des hypothèses...).

Dès lors, on recourt le plus souvent à l’échantillonnage, c'est-à-dire que l'on va chercher à comparer la moyenne obtenue dans l'échantillon avec la moyenne annoncée par le ministre. Bien entendu, la valeur trouvée sur l'échantillon n'a que très peu de chances de correspondre exactement à la valeur réelle du paramètre, même si 12/20 est la vraie valeur. Toute la question est alors de savoir si l'écart entre ces deux valeurs provient du hasard lié à l'échantillonnage, et que l'on appelle erreur d'échantillonnage, ou s'il y a une autre explication... C'est là qu'intervient le test d'hypothèse, qui nécessite de créer l'échantillon par tirage au sort et, au moins dans un premier temps, de supposer que les moyennes dans un échantillon se distribuent selon une loi normale également appelée loi de Gauss (vous savez la fameuse courbe en cloche comme ci-dessous) :

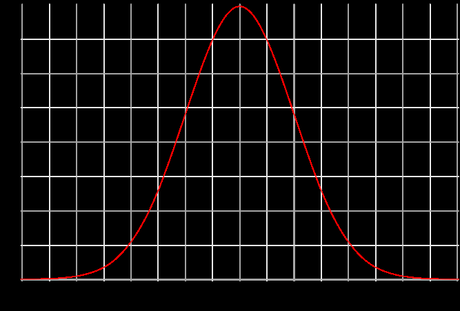
[ Source : Wikipédia ]

Mise en œuvre du test d'hypothèse dans notre exemple

Notre test doit permettre de conclure au rejet ou non de l'hypothèse H0=la note moyenne en Mathématiques en filière S est de 12/20. L'hypothèse alternative sera par exemple H1=la note moyenne en Mathématiques en filière S n'est pas de 12/20. Notre prise de décision se fera sur la base des résultats obtenus sur les échantillons, ce qui signifie que nous ne serons jamais certain à 100 % d'avoir pris la bonne décision. En fait, il existe quatre situations :

Décision/Situation H0 vraie H0 fausse

Non-rejet de H0 Bonne décision

Mauvaise décision :

erreur de 2e espèce

Rejet de H0

Mauvaise décision :

erreur de 1re espèce

Bonne décision

Avec un peu d'humour, je dis toujours à mes étudiants que l'erreur de 1re espèce (alpha) est similaire à une alarme sans feu, tandis que l'erreur de 2e espèce (bêta) correspond à un feu sans alarme. Alpha mesure en quelque sorte la confiance que nous avons dans notre alarme pour retentir lorsqu'il y a effectivement le feu. On va donc chercher à minimiser le risque d'erreur, en l’occurrence celui de 1re espèce (alpha), sachant que les deux risques sont liés. En général, on fixe alpha à 5 %, voire 1 %. Puis, le test consistera à définir une zone où, si H0 est vraie, la valeur du paramètre calculée dans l'échantillon a peu de chance s de se trouver. En pratique, comme alpha est la probabilité de rejeter H0 sachant que H0 est vraie (risque de 1re espèce), et que la distribution est supposée normale, l'on trouve les deux bornes a et b de l'intervalle de non-rejet de l’hypothèse H0.

Si la note moyenne calculée dans notre échantillon est dans l'intervalle [a;b], on ne peut pas rejeter l'hypothèse H0 au seuil alpha. En revanche, si la note moyenne est suffisamment éloignée de la moyenne testée (donc en dehors de l'intervalle [a;b]), alors on rejettera l'hypothèse H0, ce qui signifie que l'on a 5 % de chances de prendre la mauvaise décision.

C'est ainsi que se construisent la plupart des tests, qui servent tant en médecine, en biologie et dans toutes les sciences expérimentales. Vous aurez noté que certaines conditions fortes doivent être respectées (distribution suivant une loi normale, etc.), ce qui peut parfois rendre les tests moins probants lorsque l'expérimentateur se contente d'appliquer des formules sans les comprendre...