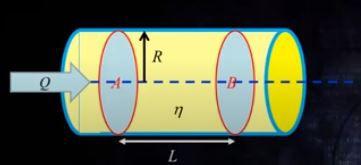
En admettant qu'un objet solide en forme de disque (de surface pi r²) fait face à un liquide en mouvement de viscosité 'eta' (η) dans un bassin, on peut considérer que le débit du fluide accélérant autour de lui est égal à la quantité de fluide qui passerait à travers lui, si cet objet était une canalisation.
Donc nous passons par la solution de Poiseuille: Q = (πr4)/(8η) x (ΔP/L), pour Q = débit du fluide.
Il faut savoir annuler la longueur dans Navier-Stokes (en abréviation N.S.), parce qu'elle est indéfinie dans les remous qui agitent un liquide après l'obstacle. Selon la méthode de la simplification des unités espace-temps, la différence de pression entre l'avant de l'obstacle et l'arrière (où se situent les remous) est justement ΔP = acc (de N.S) . L
Donc nous n'allons plus utiliser ΔP mais bien (NS. L) dans Poiseuille, pour extraire ensuite NS.
Reprenons donc Poiseuille ........... Q = (π r4)/(8 η) x (N.S . L / L)
Comme la longueur s'annule d'elle-même..
Dès lors, ......................................... Q = (π r4 x N.S ) / (8η)
On extrait ensuite Navier-Stokes........ N.S = (8 η x Q) / π r4
Or πr4 est une surface ronde S, mise au carré et divisée par π ... , donc, au final nous avons:
Navier-Stokes = ( 8 η π x Q ) / S²
Jeu de briques
Snake
Pacman
Bubble