La formule du binôme de Newton

Le problème

On souhaite disposer d’une formule générale pour développer le produit

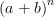
où

et sont des complexes donnés et un entier naturel.

Lorsque

, on sait faire :

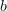
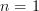
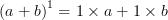
Lorsque

, on sait aussi :

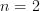
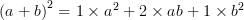
On a déjà utilisé également le développement correspondant à

:

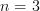
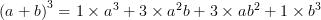
Dans le cas général, on conçoit que pour développer

, il convient de choisir, dans chacun des facteurs égaux à , soit , soit . Le résultat sera donc une somme de termes de la forme (on a choisi dans facteurs et dans les autres), avec variant de 0 à . Tout le problème est de compter combien de fois chacun de ces termes apparaît dans le développement.

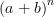
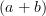
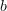
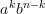
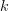
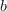
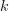
Conjecture

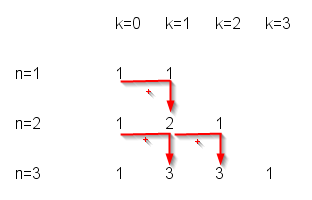
Observons les premiers coefficients qui apparaissent dans les cas particuliers ci-dessus :

Les premiers coefficients

A l’observation de ces coefficients, on remarque une propriété qui permet de calculer les termes de la ligne suivante :

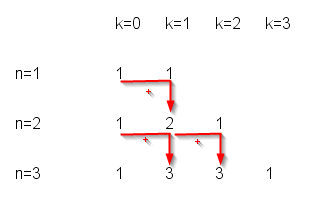
Règle de calcul

Pour écrire clairement la conjecture suggérée par la figure ci-dessus, nous avons besoin d’une nouvelle notation. Nous noterons

le nombre d’apparition du terme dans le développement.

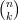
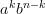
On peut donc conjecturer la propriété suivante : pour tout entier naturel

, pour tout entier variant de 1 à ,

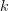
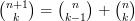
Preuve de la conjecture

Avec les notations adoptées, nous pouvons écrire :

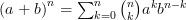
et au rang suivant :

(1).

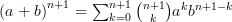
Calculons cette deuxième somme d’une autre façon :

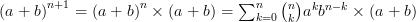
D’où

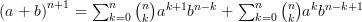
Dans la première somme, effectuons le changement de numérotation des termes consistant à remplacer

par :

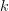
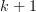
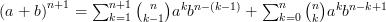
ou encore :

.

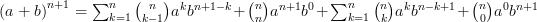
Cette écriture permet de regrouper les deux sommes en une :

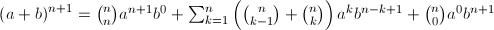
On a par ailleurs de façon évidente :

et .

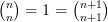
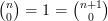
D’où finalement :

(2) .

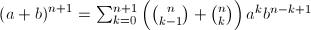
En comparant les égalités (1) et (2) ci-dessus, on obtient par identification des coefficients :

, pour tout entier naturel , pour tout entier variant de 1 à , ce qui prouve la conjecture.

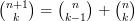
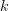
Conclusion

La formule conjecturée étant vraie, on peut calculer de proche en proche les coefficients binomiaux

pour développer des produits du type .

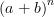
Complément : lire le billet sur le triangle de Pascal.

Wikio