Taxonomie des modéles de taux

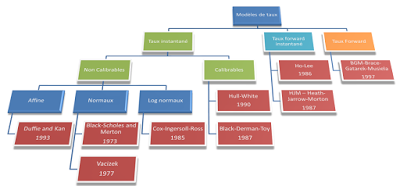
Modèles de taux: Notions.

Le plus connu des modèles mathématiques appliqué à la finance, celui de Black&Scholes, fait l’hypothèse d'un taux sans risque r0 constant dans le temps. Or comme on peut l'observer tous les jours, les taux d’intérêts fluctuent tout le temps.
Pour se projeter dans le futur, la première approche serait d'utiliser la courbe de taux Zero Coupons (voir mon article sur les swaps de taux) qui contient des taux implicites futures qui correspondent aux attentes des acteurs du marché à l'instant présent. Il faut néanmoins comprendre que cette approche a des limites: les taux implicites reflètent les attentes des acteurs du marché mais ces attentes peuvent ne pas se réaliser. Quand on parle du futur, il faut tabler sur un degré d'incertitude qui doit être expliqué par modèle probabiliste stochastique.
Ces modèles sont critiques pour tous les portefeuilles de taux et de dérivés de taux. Les équations différentielles stochastiques qui gouvernent ces modèles s’appellent des équations de diffusions, et elles sont essentielles dans toute les formes d’estimation statistiques des pertes associées à un portfolio. Par exemple: la VaR par simulation de Monte-Carlo.
La catégorisation classique consiste à distinguer les modèles Markoviens, des modèles non-Markoviens. Les modèles Markoviens ne dépendent que de la valeur présente d'une variable d'état et non de son parcours historique. 
Pour bien comprendre le sens de cette propriété, je vais prendre une des question du questionnaire de finance dont j'avais déjà parlé:

Le taux actuariel monte de 1% puis redescend de 1% immédiatement. Combien vaut l'obligation par rapport à l'instant précédent ?

Selon un modèle markovien, l'obligation vaut exactement la même prix avant et après le choc du taux actuariels de 1%. Pour un modèle non-markovien, ce n'est pas vrai en général.
Si cette classification à un sens statistique fort, elle ne permet pas de classifier les modèles, car la majorité des modèles sont Markovien par design. Par ailleurs, certains modèles sont non-Markoviens dans le cas général, mais Markoviens avec certaines fonctions de calibration de leur équation de diffusion.
Je préfère distinguer les modèles suivant la ou les variables d'état qu'ils utilisent.  Pour le praticien, la différence entre les modèles utilisant des variables d'état différente est un facteur plus distinctif.
Je prendrai la même démarche pour distinguer les modèles adaptés à la calibration et ceux qui ne le sont pas ou peu. La calibration par définition est l'adaptation des paramètres d'un modèle mathématiques aux données observées dans le monde réel. Ceci est fait typiquement en prenant un historique de valeur observables et en le comparant aux résultats du modèle pour en ajuster les paramètres. A partir de 1985, tous les modèles sont devenus hautement calibrables avec les données de marchés, ce qui n'était pas le cas des modèles précurseurs.

Définition des variable aléatoires utilisées pour modéliser les taux.

Parmi tous les modèles listés dans cet article, il n'y a que 3 variables aléatoires réelles correspondant à des valeurs de marchés qui sont utilisées: Le Short Rate (taux courts), le taux forward instantané, et le taux forward simple.

Le short rate.

Soit B(t,T) la valeur à l'instant t de l'obligation d'actualisation, il s'agit d'une obligation théorique versant 1 en T (B(T,T)=1. Si on prends une convention continue: 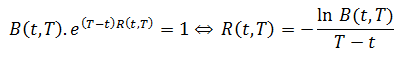Ou R(t,T) est le taux zéro coupon. On note:
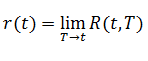Le short rate.

Le Taux forward

Le taux forward est défini comme le taux futur s'appliquant entre deux dates dans le futur [T;T+D]. On note:
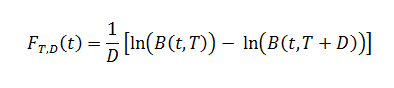On appellera F le taux forward.

Le Taux forward Instantané

Le taux forward instantané est défini comme:

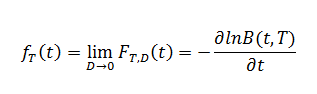
Les modèles: Ce qu'ils doivent expliquer...

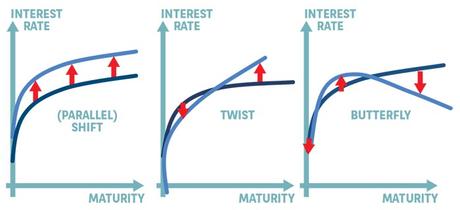
Une analyse par composante principale fait apparaitre trois composantes indépendantes des mouvements de taux:

• Le shift: un mouvement parallèle de l'ensemble des taux. Ce paramétre explique 80 à 90% de la variance de taux
• Le Twist: les taux courts et longs vont dans des directions opposées. explique 5 à 10% des variance de taux
• Le Butterfly: les taux courts et longs vont dans le même sens, mais les taux moyens évoluent en sens contraire, ceci explique en général 1 ou 2 % de la variance.

On notera que les modèles ayant une seule variable d'état (de dimension 1 en fait) sont mal adaptés à pricer les produits dépendant de la courbature des taux (Butterfly). Dans ce cas, il est souvent nécessaire de créer des modèles ayant deux ou plus variable d'état. Je vous invite à vous reporter aux annexes pour savoir quels modèles peuvent être adaptés pour avoir plusieurs variables.

Les modèles basés sur le short rate

Black Scholes & Merton (1973)
Ce modèle est dérivé de la fameuse formule de pricing des options sur actions et appliquées aux options sur obligations. Il souffre de problèmes majeurs:

• Il ne prend pas en compte l'évolution de la volatilité quand l'obligation mature
• Il permet les taux négatifs
• Le taux court terme est considéré comme constant, mais le taux long terme est stochastique
• Il ne peut être calibré.

Vacizek (1977)
Le modèle de Vacizek fait des assomptions normales sur la distribution de probabilité des taux. De fait, ce modèle peut construire des taux négatifs.Il laisse aussi la possibilité de construire des opportunités d'arbitrages. Il contient toutefois un terme de retour à la moyenne, mais il est difficilement calibrable (1 seul paramètre), et ne permet pas de s'adapter à la courbe des ZC existante à t=0. De fait, ce modèle a de très mauvaise qualité prédictives, même si il permet d'obtenir des solutions analytique pour pricer des dérivés.
Hull White (1990)
Ce modèle est construit pour être calibré aisément. avec 3 paramètres pouvant être adaptés à la courbe des taux, car Ils dépendent de t. Il est très couramment utilisé pour pricer les options américaines et les swaptions car il s'adapte particulièrement harmonieusement avec les arbres recombinatoires (Markoviens) et les lattices. Il contient un terme de retour à la moyenne. Malheureusement, cette adpation aux procédures numériques se fait aux dépends de l'obtention de solutions analytiques. Des taux négatifs peuvent aussi apparaître dans certains cas limites.
Son plus grand défaut reste toutefois la grande sensibilité des résultats aux procédures de calibration, qui peuvent induire dans le cas d'une utilisation non raisonnée à des résultats aberrants.
Black Derman Toy (1987)
Ce modèle est construit sur une la loi log-normale, ce qui garantit que les taux ne sont jamais négatifs, mais la loi log-normale est moins adaptée à des solutions analytiques. Ces modèles sont donc adaptés à des solutions numériques. Il est couramment utilisé pour construire des méthodes de pricing par arbres binomiaux ou on apprécie sa capacité à se calibrer à partir des prix des caps et swaptions.

Les modèles basés sur le forward rate instantané.

Il s'agit des modèles de Ho & Lee dans le cas discret et surtout de Heath,Jarrow & Morton (1987) dans le cas continu. Ici la variable d'état est de dimension infinie. Il s'agit d'un système d'équation de diffusion liée à une maturité précise. On essaie de construire le vecteur stochastique {f_T(t)} avec 0<t<T. Ou f(t,T) est le taux forward instantané en T.
Ce qui est notable dans ce choix de variable d'état, c'est que f_T(0) est directement observable, il s'agit de la courbe des taux forwards. la calibration de ce modèle est donc particulièrement aisée.
Un autre point important à noter est que Heath, Jarrow & Morton ont fait une contribution importante en permettant d'exprimer le drift de leur équation de diffusion en fonction de leur fonction de volatilité, de sorte que seul ce paramètre devra être précisé pour obtenir la calibration. Par ailleurs, notons que HJM apporte deux contributions manquantes dans Ho&Lee: l'absence d'opportunité arbitrage et la possibilité de calibrer le modèle pour qu'il soit markovien.

Le modèle basé sur le forward rate.

Il s'agit du modèle Brace-Gatarek-Musiela (BGM)  aussi appelé LIBOR market Model (LMM) qui modélise les taux forwards directement observables sur les marchés.
Dans la pratique, les taux forwards sont ceux du LIBOR 3 mois. De sorte que modéliser la courbe des taux sur 20 ans, nécessite de trouver un vecteur de 4*20=80 variables stochastiques.
Ce modèle non markovien répond au critiques qui entachaient les modèles précédents:

• Pas d'arbitrages.
• Calibration par la courbe complète des taux forwards observés en t=0.
• Multi facteurs.
• La structure de la volatilité forward est respectée

La contrepartie de ces avantages est que ce modèle ne permet pas en général d'obtenir des solutions analytique pour le pricing, il est uniquement adapté à des méthodes numériques.

Annexes

Modelling the term structure of interest rates: a review of the literrature.
R. Gibson, F.-S. Lhabitant, D. Talay
LIBOR market model
Andrew Lesniewski