4.4 Harmonies polyédriques

En raisonnant avec un peu d’abstraction, nous allons découvrir que les objets situés à proximité du polyèdre ont des caractéristiques formelles communes, qui s’estompent d’autant plus qu’on s’éloigne de l’objet de base.

Ainsi la « transformation » qui est en train d’affecter le polyèdre résonne, de manière plus ou moins directe, sur les objets voisins : sortes d’harmoniques formelles, similaires à des harmoniques sonores.

Tout ce chapitre est un SCOOP.

L’échelle (première harmonique)

L’étirement du cube

Reprenons le schéma de la transformation de Dürer. Posons le cube de côté 1 sur sa pointe et traçons, en vue de face,  un quadrillage dans lequel l’inscrire : il va avoir une largeur Rac(2) (la diagonale du carré) et une hauteur Rac(3) (la diagonale du cube). Mais surtout, il va se découper naturellement en six tranches horizontales, correspondant aux points significatifs du contour.

L’échelle à six intervalles

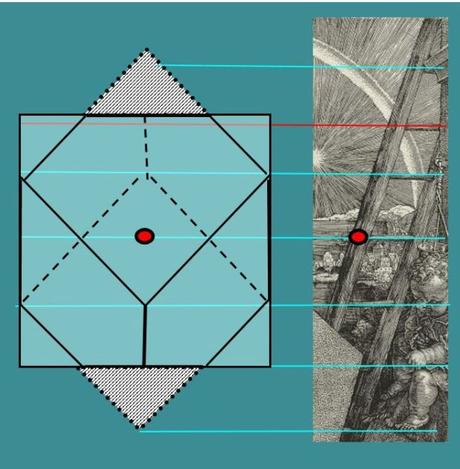
Les six intervalles de l’échelle font directement allusion aux six tranches horizontales du quadrillage. Mais de plus, l’inclinaison de l’échelle montre directement l’étirement en cours. Il suffit d’imaginer qu’elle est en train de se relever : les tranches vont encore s’élargir jusqu’à ce qu’elle atteigne la position verticale : alors le facteur d’étirement sera 2, et le cube se sera transformé en octaèdre. (Le calcul montre que l’angle initial de l’échelle, au début de la transformation, devrait être de 41,5°, pour qu’il atteigne 18° (PI/10) pour un étirement d’environ 1,27, puis 0° pour un étirement de 2).

Ceci donne peut être la solution définitive au facteur d’étirement du polyèdre : Dürer l’a réglé de manière à ce que l’échelle, qui matérialise la transformation de Dürer, montre l’angle de PI/10.

Le nombre d’or ne se cache pas dans le polyèdre, mais dans l’échelle !

Les tranches à ôter

Remarquons que les deux intervalles extrêmes de l’échelle sont partiellement masqués, en haut par le bâtiment,  en bas par le polyèdre. Or ce sont justement ces intervalles qui correspondent, dans l’état actuel de la transformation, aux tranches qui ont déjà été ôtées.

L’idée de manque de matière, côté volume, se traduit donc visuellement,

côté échelle, par l’idée d’un « manque de jour ».

Une preuve manifeste de l’importance du nombre d’intervalles et de leur écartement est que Dürer, pour laisser la place à l’échelle, a dû pratiquer une sorte d’encoche dans le parapet.

Il est étonnant que le rapport étroit entre le polyèdre et l’échelle – objet qui le touche pourtant directement, n’ait pas été remarqué jusqu’ici ; alors que le rapport du polyèdre avec le carré magique, qui est pourtant moins évident, est connu depuis 1980.

C’est sans doute parce que dans l’échelle, les commentaires se focalisent plutôt sur les sept barreaux que sur les six intervalles, tant l’oeil est attiré par les pleins plutôt que par les vides.

La balance (deuxième harmonique)

Nous allons maintenant nous éloigner du polyèdre et fixer notre attention, un peu plus à droite, sur la balance.

Les plateaux retournés

Dürer a dessiné avec une grande précision l’entrecroisement des trois cordes de chaque plateau. Le plateau de droite est croisé une seule fois, c’est à dire qu’il suffirait de  le retourner vers le bas pour décroiser ses attaches. Le plateau de gauche, lui, est croisé de manière plus complexe : mais en le retournant deux fois, c’est-à-dire en le remettant dans sa position naturelle, on démêle les attaches  (on pourra s’en convaincre en réalisant un petit modèle, avec trois bouts de ficelle et un rond de carton).

Une copie d’après-nature ?

Pourquoi cette dissymétrie, qui fait que le plateau de droite, pour décroiser ses liens, doit devenir un « anti-plateau » (ouvert vers le bas) ? Peut-être est-ce fortuit : nous avons vu que dans le dessin préparatoire, l’entrecroisement des cordes est exactement le même, tandis que le fléau est vu sous une perspective différente : peut-être Dürer s’est-il contenté de faire le croquis d’une balance qu’il avait sous la main, et dont un des plateaux était monté à l’envers. Et peut-être  a-t-il retourné deux fois le plateau de gauche, juste pour montrer la précision de son dessin ?

Un second paradoxe

Que Dürer ait copié ou pas une balance existante, au final ce jeu avec les fils illustre deux nouveaux paradoxes.

• D’une part, un paradoxe de l‘identité : deux objets qui se proclament égaux peuvent être des inverses (un plateau et un anti-plateau).
• D’autre part, un paradoxe de la complexité :  le noeud le plus imbriqué s’élimine de lui-même, alors que le noeud le plus simple se révèle irréductible.

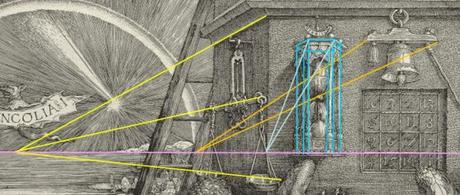
Triangles opposés

Les points d’attache des trois cordes dessinent, sur chaque plateau, un triangle équilatéral (en vert). On voit aisément que ces triangles sont opposés. En outre,  le triangle du plateau de gauche est disposé comme le triangle de la face supérieure du polyèdre (noté 2), tandis que celui de l’autre plateau est dans la même position que celui de la face inférieure (noté 1).

Un modèle du polyèdre

Cette analogie entre les plans de coupe du polyèdre et les plateaux de la balance est plus qu’une coïncidence. Voyons les choses en mouvement : inclinons le fléau, et laissons-le revenir vers l’équilibre : les deux plateaux vont se rapprocher l’un de l’autre, à l’image des plans de coupe durant la transformation de Dürer.

Mais il y a plus. Ne touchons plus au fléau, mais continuons  à retourner les plateaux sur eux-mêmes  (flèches violettes) :  les cordes vont se raccourcir, et l’angle au sommet va devenir moins aigu, jusqu’à épouser celui du polyèdre.

Les cordes des plateaux donnent une image filaire des deux pyramides fantômes (en bleu).

Et la  perspective ?

Si nous avons remarqué l’équivalence entre les triangles des plateaux (gauche et droit)  et les faces (supérieure  et inférieure) du polyèdre, c’est que nous avons fait abstraction de la perspective. Tenons-en compte maintenant, et traçons les lignes de fuite passant par les points d’attache des six cordes : nous constatons que le plateau qui est orienté comme la face supérieure du polyèdre, c’est maintenant  le droit (en jaune) ; tandis que le gauche est orienté comme la face inférieure.

A l’analyse, la balance se révèle un objet particulièrement subtil, car son sens lui est donné, non par la main du dessinateur, mais par le regard que le spectateur va porter sur elle.

• Qu’il la considère localement, comme un objet isolé de son contexte : il  percevra les plateaux comme déséquilibrés, et  il les associera d’une première manière avec les plans de coupe du polyèdre (il trouvera une correspondance gauche/haut et droite/bas).
• Qu’il rectifie son regard en tenant compte de la perspective : les plateaux reviennent à l’équilibre, et la correspondance entre plateaux et plans de coupe s’inverse.

Voici donc un instrument qui est tout à la fois juste et injuste ; semblable au polyèdre et semblable au polyèdre retourné. Ses plateaux sont à la fois des égaux et des inverses ; quand aux noeuds, le plus compliqué ne noue rien, et le plus simple noue absolument.

La balance de Melencolia n’est pas un instrument de pesée  :

c’est un instrument de pensée, un modèle pour la conciliation des contraires.  

Le sablier  (troisième harmonique)

Continuons à nous éloigner du polyèdre en nous dirigeant vers la droite : nous voici au sablier.

Un  problème de perspective

La base du sablier est vue comme une ligne, ce qui est normal puisqu’elle se situe sur la ligne d’horizon. Les quatre colonnes frontales, plus les deux colonnes que l’on devine derrière, permettent de reconstituer l’hexagone de la face supérieure. On se rend alors compte que la perspective de cet hexagone correspond à un point de fuite différent du point de fuite principal : il est bien sur la même horizontale mais beaucoup plus à droite, sur l’arête du bâtiment (en bleu sur le schéma).

Le sablier n’est pas le seul objet qui échappe à la perspective : si l’on regarde la cloche (située portant encore plus à droite), le rectangle allongé à la base de la pièce de bois correspond à un troisième point de fuite (en orange), situé entre les deux.

Pourquoi Dürer, si à cheval sur la perspective, s’est-il permis cette liberté ?  Le sablier, construit à la même place selon une perspective correcte, n’aurait montré que deux de ses faces et trois de ses colonnes, rendant plus difficile sa lecture comme un objet hexagonal. Nous touchons ici à un point important de la méthode de Dürer : la rigueur de la perspective est un alibi, un trompe-l’oeil, qui s’efface au besoin devant un intérêt supérieur. Ce qui est important ici, c’est que le sablier soit bien positionné à cet emplacement dans la gravure, entre la balance et la carré (nous verrons pourquoi dans 8 Comme à une fenêtre ) ;  et que le spectateur comprenne bien qu’il est hexagonal.

Un autre modèle du polyèdre

Vu du haut, la symétrie hexagonale du sablier, à laquelle Dürer attache tant d’importance, est évidemment un indice pour le rapprocher du polyèdre. Le fait que celui-ci soit symétrique entre le haut et le bas est une autre similitude.

Mais il y a une dernière affinité, plus subtile, qu’on ne perçoit qu’une fois qu’on a compris que le polyèdre ne représente pas un objet achevé, mais un instantané dans un processus en devenir. Le polyèdre évolue en diminuant son angle au sommet, et en rapprochant ses surfaces de coupe (deux triangles qui deviennent de plus en plus grands).

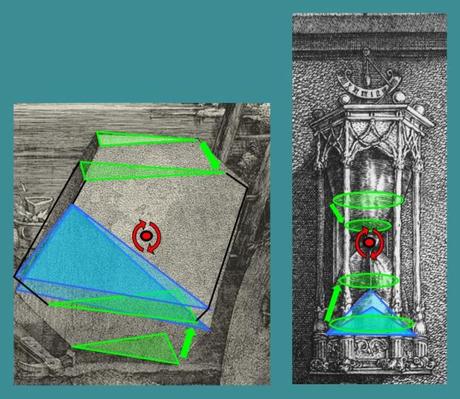
De même le sablier nous montre, dans son compartiment du bas, un cône de sable qui grandit en modifiant son angle au sommet  (cette fois en l’augmentant) ; et si nous tapotons les parois de verre pour égaliser les niveaux, nous verrons, dans les deux compartiments,  deux surfaces qui se rapprochent l’une de l’autre (cette fois circulaires, en devenant de plus en plus petites).

Le sablier est triplement en affinité avec le polyèdre :

• par sa géométrie (symétrie hexagonale),
• par son utilisation (retournement haut-bas),
• et par sa dynamique interne (modification de l’angle au sommet, et rapprochement des plans de coupe).

Le carré magique (quatrième harmonique)

Nous avons vu que le Polyèdre se projette orthogonalement dans deux quadrillages carrés.

Mais comme le Sablier et le Carré sont deux harmoniques du polyèdre, ils se ressemblent également entre eux.

Ainsi, les nombres de la moitié haute étant symétriques de ceux de la moitié basse, retourner le Carré de bas en haut ne modifie pas ses motifs numériques.

Notons également qu’en reliant les chiffres pairs et les chiffres impairs entre eux, on obtient deux familles d’hexagones.

.

Des outils pour construire le polyèdre

Le polyèdre est un objet abstrait : pour le construire, scie, marteau ou meule sont inutiles.

Ce qu’il faut, ce sont des instruments de la pensée, des Idées.

• L’échelle penchée règle son étirement vertical.
• Les plateaux de la balance suggèrent les triangles de coupe.
• Le sablier donne sa forme en plan, un hexagone.
• Enfin, le carré nous donne ses projections dans deux directions.

Des rotations croissantes

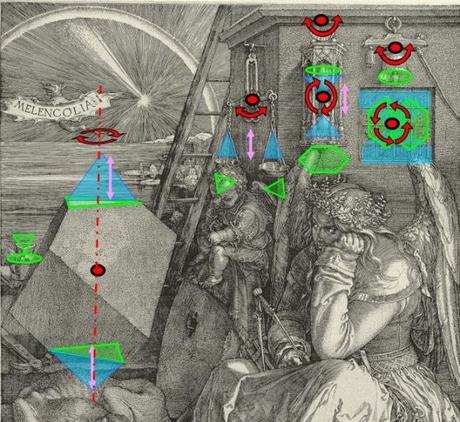
Tous ces objets ont pour caractéristique commune de posséder un centre de rotation, autour duquel ils trouvent leur équilibre. Mais les possibilités et de rotation s’accentuent de la gauche vers la droite :

• le polyèdre est bloqué sur son axe vertical, dont il ne peut pas dévier ;
• l’échelle peut s’incliner un peu sans perdre son équilibre ;
• le fléau de la balance autorise des inclinaisons plus marquées ;
• même amplitude pour la cloche ;
• sur le cadran solaire, l’ombre de l’aiguille décrit un quart-de-tour durant la journée ;
• le sablier est fait pour être retourné d’un demi-tour ;
  
• le carré peut par définition être tourné d’un quart-de-tour sans qu’il perde ses propriétés numériques.

Des mouvements cycliques

• Le polyèdre peut indéfiniment se transformer, du cube et l’octaèdre et retour ;
• l’échelle peut être montée ou descendue ;
• la balance et la cloche oscillent ;
• l’ombre de l’aiguille tourne et croît, de la même manière chaque jour,
• tandis que le sable recommence à s’écouler à chaque retournement du sablier ;
• le carré compte et recompte à l’infini les nombres de un à seize.

Le bas comme le haut

Enfin, et c’est leur caractéristiques la plus forte, tous ces objets portent l’idée de la communication entre le bas et et le haut. Voire même de l’interaction entre ces deux mondes.

• L’échelle donne accès, sans barrière, à l’étage supérieur ;
• des plateaux de la balance, l’un monte quand l’autre descend, indiquant que les deux trajets sont possibles ;
• le sable remplit progressivement le compartiment bas, sans qu’un grain ne se perde ;
• l’aiguille reproduit, en minuscule, la marche du soleil ;
• le carré magique donne une image parfaite de l’équivalence entre le haut et le bas : chaque nombre de la moitié basse a son jumeau dans la moitié haute, qui l’équilibre exactement pour le compléter à 17 ; décaler un nombre dans le  compartiment du haut perturbe instantanément le compartiment du bas ;
• quant au polyèdre, il possède une propriété bien particulière, qui fournit également une image forte de la solidarité entre le  haut et le bas ; car pour que sa moitié haute s’interchange avec sa moitié basse, nul besoin de le retourner de haut en bas: il suffit de le faire pivoter d’un tiers de tour autour de son axe vertical.